NOÇÕES DE FUNÇÃO POR MEIO DE CONJUNTOS

Olá pessoal! Tudo certo?

Antes de tomarmos uma decisão importante, é sempre interessante observarmos o caso sob diversos pontos de vista, não é? Existem alguns assuntos da matemática onde é possível fazer exatamente isso, e é por esse motivo que iremos estudar a noção de função sob o ponto de vista dos conjuntos no texto de hoje! Compreender direitinho o conceito de função, pode nos ajudar a entender melhor as funções afim, quadrática, modular, exponencial, logarítmica, e também nos auxilia a melhorar a interpretação, que tem sido cada vez mais cobrada nas questões interdisciplinares do ENEM e também nos mais diversos vestibulares.

E vocês, querem saber tudo sobre as funções matemáticas? Então assinem a plataforma do Professor Ferretto! Lá, todas as funções que acabamos de citar possuem um módulo de ensino exclusivo, com videoaulas, exercícios de manipulação, questões do ENEM e de vestibulares resolvidas em vídeo, e o melhor, vocês podem acompanhar seu desempenho através das estatísticas individuais e do ranking do curso que desejam realizar! Saibam mais acessando o site!

Chegou a hora de iniciarmos os estudos! Mas caso vocês não façam ideia do que é um conjunto, e de como podemos representa-lo, não tem problema, eu tenho uma solução! Deem uma olhadinha no texto Introdução aos Conjuntos, e aí eu lhes dou certeza que tudo o que vamos ver na sequência ficará bem claro.

Bom, nós vamos tratar agora da noção de uma função por meio de conjuntos. Isso significa, que abordaremos como uma função pode ser formada em meio a dois conjuntos. Basicamente nós temos uma função, quando é possível associar cada um dos elementos do conjunto de partida a um único elemento do conjunto de chegada.

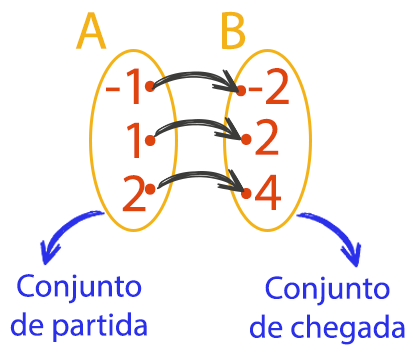
No exemplo acima, é possível visualizar dois conjuntos representados na forma de diagrama. Um certo conjunto A, é dado como o conjunto de partida, enquanto que o outro, o conjunto B, é dado como conjunto de chegada. Se observarmos a figura com mais atenção ainda, nosso olhar será conduzido a algumas setas que estão “ligando” cada elemento do conjunto A a um certo elemento do conjunto B. É exatamente esse o tipo de ligação que deve ocorrer para que o sistema se caracterize como uma função!

Certo, mas por que exatamente os elementos -1, 1, e 2, do conjunto A, estão sendo ligados respectivamente a -2, 2, 4, do conjunto B, quer dizer, qual é a relação entre esses elementos? A relação utilizada para associar os elementos dos dois conjuntos é conhecida como lei de correspondência, e se vocês observarem os cálculos abaixo, já ficará mais claro qual foi a lei de correspondência utilizada nesse exemplo:

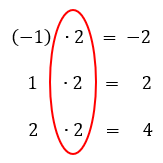
Se nós multiplicarmos todos os elementos do conjunto A por 2, ou seja, se obtermos o dobro desses valores, nós encontraremos os elementos de B! Incrível não é mesmo? Por isso, podemos dizer que a lei de correspondência do nosso exemplo está associando cada elemento de A ao seu dobro, em B.

Ficaram ligados no que eu disse aí em cima? Pois é, nem nos conjuntos tudo é perfeito! Nem sempre os conjuntos de partida e de chegada vão ter o mesmo número de elementos, e nem sempre vamos conseguir efetuar ligações entre todos os elementos. O fato é que não importa se restarem elementos sem ligação no conjunto de chegada, só não podem restar elementos no conjunto de partida. E ainda, para que uma função exista, cada elemento do conjunto de partida deve ter apenas um único elemento correspondente no conjunto de chegada, ou seja, apenas uma única setinha deve sair de cada elemento do conjunto de partida rumo a um dos elementos do conjunto de chegada.

Entendido até aqui? Fiquem tranquilos porque agora nós iremos resolver alguns exemplos para tornar a ideia mais clara:

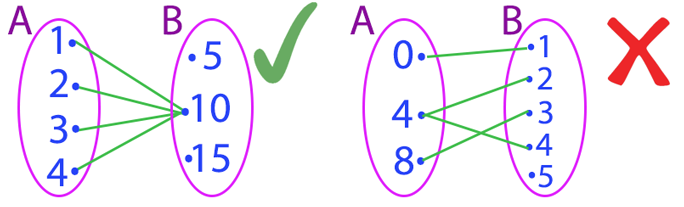
Sejam os conjuntos A = {1, 3} e B = {2, 3, 4}, associar cada elemento de A a um valor maior em B.

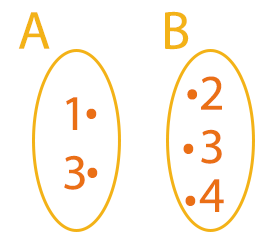
Observem que se a lei de correspondência desse exemplo, nos pede para associar cada elemento de A a um certo valor de B. Isso quer dizer que A é nosso conjunto de partida e B o nosso conjunto de chegada. O que precisamos fazer primeiramente, é verificar se os elementos do conjunto A possuem valores maiores do que eles no conjunto B.

2, 3, e 4 são valores maiores que 1

4 é um valor maior que 3

A partir dessas informações, podemos realizar as ligações nos diagramas:

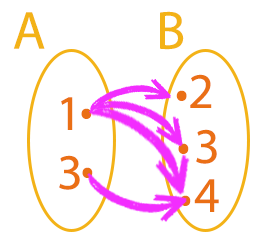
Observando as ligações, podemos concluir que não restou nenhum elemento sem ligação no conjunto de partida, até aí tudo certo! Mas vejam que apesar de o elemento 3, do conjunto A estar associado a apenas um único elemento do conjunto B, o elemento 1, do conjunto A, possui 3 elementos correspondentes no conjunto B. Portanto esse exemplo não se caracteriza como uma função!

Sejam os conjuntos A = {0, 1, 2} e B = {1, 2, 3, 4}, associar cada elemento de A ao seu igual  valor em B.

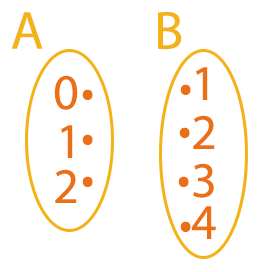
Novamente, através da lei de correspondência desta questão, nós podemos entender que A é o conjunto de partida e B o de chegada. Contudo, parece que vamos enfrentar alguns problemas aqui, afinal, devemos associar cada elemento de A ao seu valor igual em B. Bom, os elementos 1 e 2, do conjunto A, possuem os elementos correspondentes em B, 1 e 2 também. Mas e o elemento zero? Observem as ligações realizadas nos diagramas:

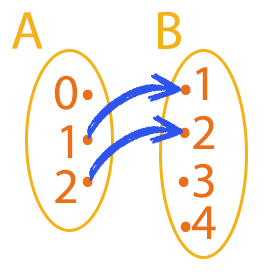
Pois é, apesar dos demais elementos do conjunto A possuírem apenas um único elemento correspondente em B, como deve ser, o elemento zero ficou sobrando no conjunto de partida, sem ligação alguma, e isso jamais pode acontecer. Por isso, esse exemplo também não caracteriza uma função!

Repararam que eu nem comentei que os elementos 3 e 4, do conjunto B, também ficaram sem ligação alguma? É porque realmente, o fato de restarem elementos sem ligação no conjunto de chegada não é um fator determinante na formação de uma função!

Certo pessoal!? Agora que já estudamos o que deve acontecer para que possamos formar uma função, vamos estudar a sua definição e notação matematicamente falando. Vem, comigo aqui!

1. DEFINIÇÃO E NOTAÇÃO DE UMA FUNÇÃO

Dados dois conjuntos A e B, uma função de A em B é uma regra que indica como associar cada elemento x ϵ A a um único elemento y ϵ B.

Definição entendida? Quase né? Vamos esmiuçar tudo que está sendo dito aí em cima para não restarem dúvidas. Vejam que se fala em dois conjuntos A e B, ou seja, devem sempre existir dois conjuntos no sistema, assim um será o de partida e o outro será o de chegada. Mas como sabemos qual deles é o de partida e qual é o de chegada? Mais um pedacinho da definição nos explica isso: uma função de A em B. Se a função é de A em B, significa que ela está partindo de A e indo até B, e por isso A é o conjunto de partida e B é conjunto de chegada.

A função é uma regra que indica como associar cada elemento x ϵ A a um único elemento y ϵ B. Isso significa que os elementos do conjunto A, ou de partida, serão os valores de x e que os elementos do conjunto B, ou de chegada, serão os valores de y, como mostram os diagramas abaixo:

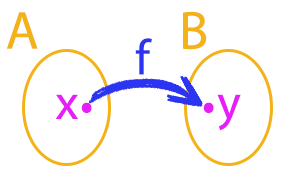
Assim, nós teremos uma função sendo aplicada aos valores de x que resultará nos valores y. Em símbolos nós podemos dizer que:

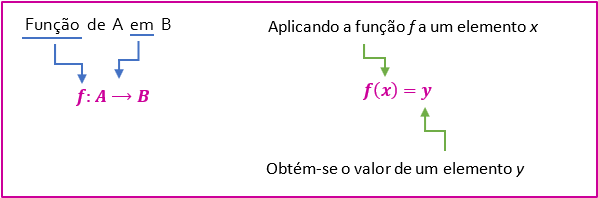
Ficou claro porque geralmente as funções são denominadas por f(x) ou por y? Tem tudo a ver com a ideia de conjuntos! Ainda, é importante repararmos que a forma de representar uma função de A em B, com a setinha apontando para B, torna ainda mais claro que A é conjunto de partida e que B é o conjunto de chegada!

Que tal aplicarmos tudo isso que acabamos de aprender em um exercício? Vamos lá!

Dados os conjuntos abaixo, faça um diagrama e diga se f é uma função de A em B, sendo x ϵ A e y ϵ B:

A = {-2, 1, 2} e B = {-4, 1, 4}

y = x²

Vamos começar desenhando os diagramas dos conjuntos A e B. Novamente, de acordo com o enunciado, já que buscamos uma função de A em B, A é o conjunto de partida, e B, é o conjunto de chegada.

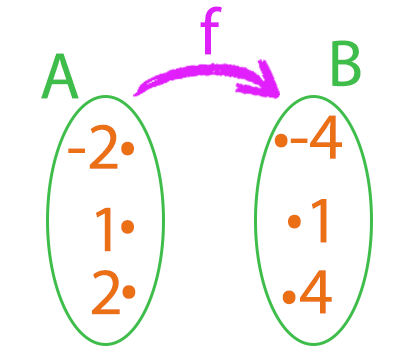
Agora, para determinarmos se f é de fato uma função de A em B, precisamos aplicar os valores dos elementos do conjunto A, na nossa lei de correspondência, y = x². Como sabemos que os valores de x pertencem ao conjunto A, e que os valores de y pertencem ao conjunto B, nós vamos substituir o valor de x na expressão por cada um dos elementos do conjunto A. De posse dos resultados, nós verificaremos se o conjunto B possui esses elementos, e faremos as ligações no diagrama.

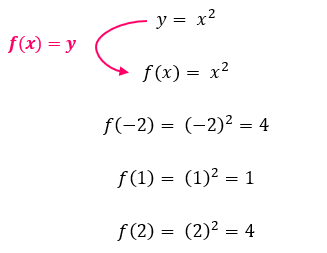
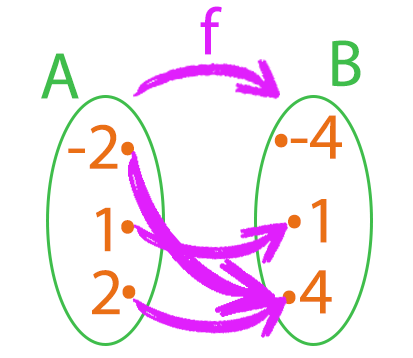
Só haverá uma função aqui, se todos os elementos de A tiverem um único elemento correspondente em B. Observando o diagrama, vocês acham que f é uma função de A em B? Poderíamos pensar nas seguintes hipóteses:

1. Está sobrando um elemento no conjunto B, por isso, f não é uma função.
2. Dois elementos do conjunto A são correspondentes ao mesmo elemento no conjunto B, portanto, f não é uma função.

Será mesmo? Vejam que não restou nenhum elemento no conjunto A ou no conjunto de partida, sem ligação, e é isso que importa, não há problema quando restam elementos apenas no conjunto de chegada. Além disso, apesar de dois elementos de A serem correspondentes ao mesmo elemento de B, há apenas uma única seta saindo de cada elemento de A.

Assim, só nos resta concluir duas coisas: a primeira é que sim, f é uma função de A em B! E a segunda é que como sempre, chegamos ao final do nosso texto! Pessoal, espero mesmo que vocês tenham gostado de tudo que aprendemos hoje, e que isso contribua bastante para os seus estudos! Hoje, mais do que nunca, eu os aconselho a dar uma olhadinha no vídeo que deixo em anexo. Lá vocês encontram vários outros exercícios resolvidos, e para não restarem dúvidas, quanto mais exemplos, melhor!

Um abração a todos vocês! Até breve!