NOÇÕES BÁSICAS DE PLANO CARTESIANO

Olá pessoal! Tudo bem?

O plano cartesiano é um sistema utilizado para especificar pontos e determinar localizações ou posições dentro de determinado “espaço” ou superfície. Ele é aplicado a diversas áreas do conhecimento, e na matemática, é muito importante para os conteúdos de funções, geometria analítica, polinômios e todos aqueles assuntos que envolvem a construção de gráficos. Vocês verão nesse texto, que o conceito de plano cartesiano é extremamente simples, mas se alguns detalhes não forem conhecidos, o desenvolvimento correto de uma questão que o envolva pode ficar comprometido. E não é isso que queremos quando estamos prestes a realizar as provas dos vestibulares e do ENEM, não é mesmo?

Ainda falando dessas provas, vocês sabiam que existe um plataforma de ensino 100% online, em que é possível criar um plano de estudos com foco no estudo da matemática do ENEM e/ou dos vestibulares? É a plataforma do Professor Ferretto! Lá vocês encontram todo o conteúdo de matemática do ensino médio, e também aulas de aprofundamento, para aqueles concursos com nível de exigência mais elevado. E caso surgirem dúvidas, é só contar com a ajuda dos monitores, disponíveis no plano diamante! Acessem o site para saber mais!

E agora, com muita alegria, lhes apresento o plano cartesiano!

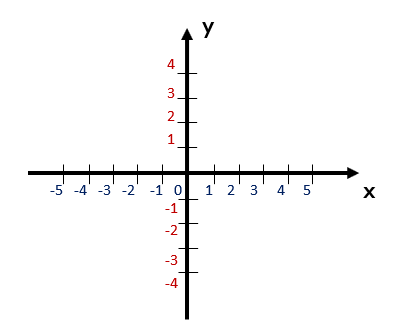
O plano cartesiano é formado por duas retas numéricas perpendiculares entre si. Isso significa que onde as duas retas se interceptam, é formado um ângulo reto, ou seja, um ângulo de 90°. Mas esse fato tão importante não poderia simplesmente passar despercebido. É por isso que esse único ponto onde as duas retas se cortam é chamado de origem do plano cartesiano.

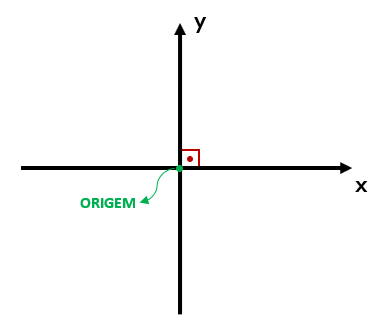
A verdade, é que quando se fala em plano cartesiano, essas retas numéricas perpendiculares possuem um nome específico: elas são chamadas de eixos, e mais especificamente de eixo horizontal e eixo vertical. O eixo horizontal também é conhecido como eixo x, ou eixo das abscissas, enquanto que o eixo vertical, também é chamado de eixo y ou eixo das ordenadas.

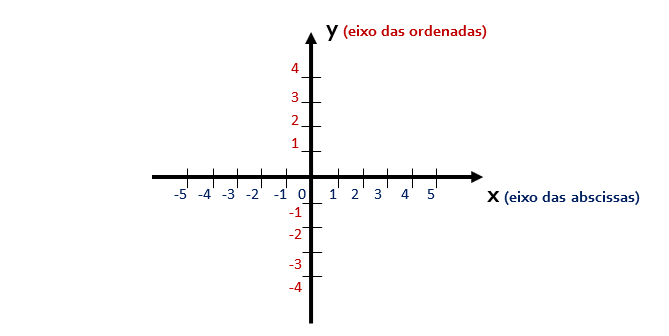
Agora, observem com atenção os eixos ou retas numéricas acima. Se tomarmos como exemplo o eixo x, veremos que a direita da origem os seus valores são sempre positivos e crescentes, e que por sua vez, os valores a esquerda da origem são sempre negativos e decrescentes. O raciocínio é o mesmo para o eixo y: acima da origem existem apenas valores positivos e crescentes, enquanto que abaixo da origem existem apenas valores negativos e decrescentes. Mas de uma maneira geral, os valores tendem a crescer para cima, no eixo y, e para a direita no eixo x. É por isso que existe uma seta apontando para esses dois sentidos nos seus respectivos eixos: é uma convenção representar as setas apontando para o sentido crescente dos valores numéricos.

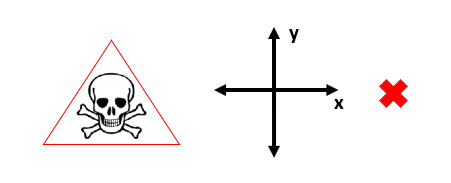
Quando não estamos muito acostumados com o plano cartesiano, corremos o risco de representá-lo com setas que apontam para ambos os sentidos dos eixos x e y. Mas isso é extremamente perigoso, como mostra a figura acima, porque está errado. As setas devem apontar sempre para o sentido positivo ou crescente dos eixos das abscissas e das ordenadas!

Depois de falarmos bastante sobre os eixos do plano cartesiano, é fato eles dividem o plano como um todo em quatro regiões. Essas regiões são chamadas de quadrantes, e por isso, deve ser do conhecimento de vocês que um plano cartesiano possui quatro quadrantes.

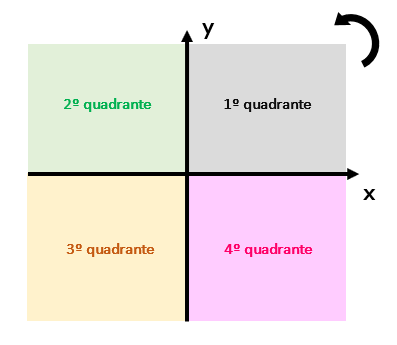
Pessoal, isso é bastante simples! Vejam que o 1º quadrante ou quadrante 1, está localizado onde todos os valores dos eixos x e y são positivos. Memorizem a posição desse quadrante! Aí, é só seguir pelas regiões no sentido anti-horário para encontrar o 2º, o 3º e o 4º quadrante! Viram como é fácil? Mas vocês também podem se basear nos valores numéricos dos eixos para se localizar. Em cada quadrante, os valores de x e de y podem ser positivos (maiores do que zero), ou negativos (menores do que zero) como mostram as definições abaixo:

1º quadrante: x > 0 e y > 0

2º quadrante: x < 0 e y > 0

3º quadrante: x < 0 e y < 0

4º quadrante: x > 0 e y < 0

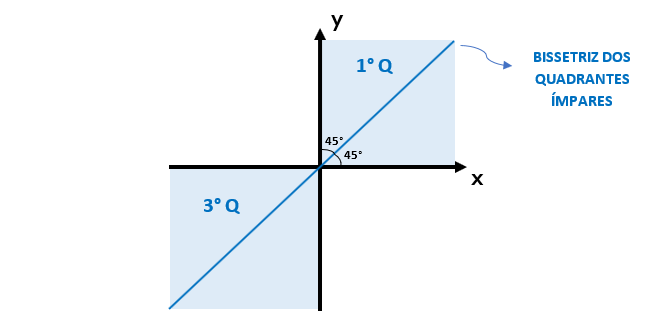
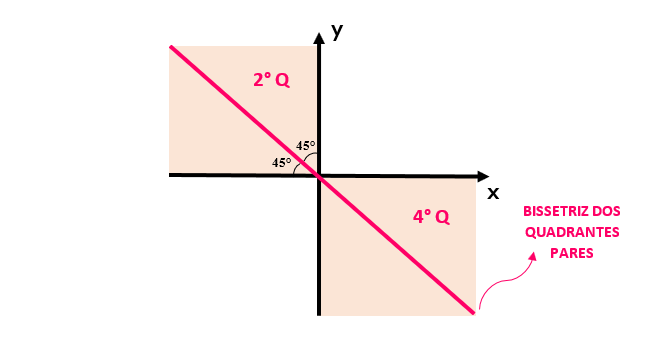
Além disso, é imprescindível conhecermos o seguinte detalhe: o número dado a cada um dos quadrantes, os divide em dois grupos distintos: os números 1 e 3 são números ímpares, por isso o 1º e o 3º quadrante são conhecidos como quadrantes ímpares. O mesmo é válido para os quadrantes restantes: como 2 e 4 são números pares, temos que o 2º e o 4º quadrante são chamados de quadrantes pares. Assim se uma certa reta cortar os quadrantes ímpares bem ao meio, dividindo pela metade o ângulo de 90º formado pelo cruzamento dos eixos x e y, diz-se que essa reta é denominada bissetriz dos quadrantes ímpares. É claro, que se a mesma reta cortar ao meio os quadrantes pares, ela será conhecida como bissetriz dos quadrantes pares. Observem as figuras para que fique bem claro:

Neste momento nós já conhecemos boa parte dos conceitos relacionados ao plano cartesiano. Mas vocês lembram que foi dito lá no início do texto, que o plano cartesiano é um sistema utilizado para especificar pontos? Pois é, a verdadeira função do plano cartesiano é mesmo se utilizar dos eixos x e y e dos seus 4 quadrantes para representar pontos, as chamadas coordenadas cartesianas. Essas coordenadas são dadas por meio de pares ordenados, na forma P(x, y). O primeiro elemento do par ordenado P, deverá representar sempre o valor que será marcado em relação ao eixo x, enquanto que o segundo elemento do par ordenado P, representará sempre o valor que será marcado em relação ao eixo y.

Um tanto confuso, não é mesmo? Por isso, nada melhor do que realizar a representação geométrica de alguns pontos no plano cartesiano para esclarecer essa ideia. Assim, dadas as coordenadas abaixo, o “segredo” é encontrar nos eixos x e y, respectivamente, o valor da coordenada x, depois o valor da coordenada y, e em seguida, ligar esses valores através de retas tracejadas. Na medida em que as retas se cruzarem, ou que houver a intersecção entre as retas, teremos ali a localização dos pontos especificados.

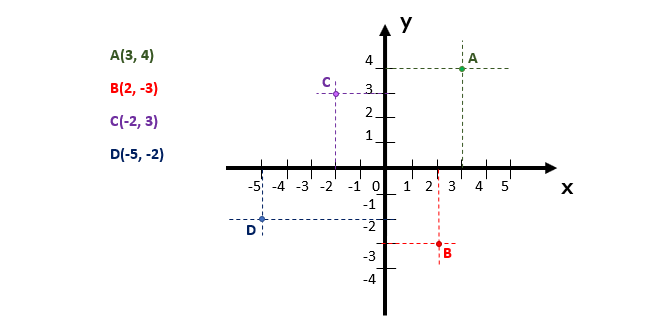
Tranquilo, não é? Assim, podemos dizer, por exemplo, que 3 é a abscissa de A, ao mesmo tempo em que 4 é a ordenada de A. Isso pode ser feito para os demais pontos ilustrados, portanto é fato que 2 é a abscissa de B, e que -3 é a ordenada de B. Vocês poderão encontrar essa forma de se referir as coordenadas cartesianas em alguns exercícios. Agora, fiquem atentos a essa dica bem importante!

A forma como descrevemos os pontos ou coordenadas do plano cartesiano é chamada de par ordenado, porque a ordem em que os elementos são dispostos importa, diferente do que acontece quando os elementos de um conjunto são representados, por exemplo. Um certo conjunto A = {1, 2} possui os mesmos elementos que um certo conjunto B = {2, 1}, que são os valores 1 e 2, ou seja, aqui, a ordem da representação não mudou nada. Mas quando se fala em coordenadas, dado o par ordenado A(1, 2), tem-se que a coordenada de A em x é de valor 1 e que a coordenada de A em y é de valor 2. Do contrário, ou seja, dado o par ordenado B(2, 1), tem-se que a coordenada de B em x é de valor 2 e que a coordenada de B y é de valor 1. Vamos representar esses dois pares ordenados no plano cartesiano abaixo, para vocês verem como se confundir com a ordem dos valores pode gerar pontos em localizações bem diferentes, e portanto, causar um erro grave!

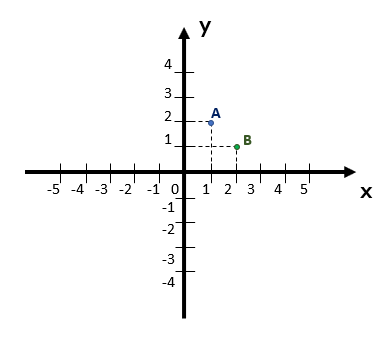
Estamos chegando ao final do nosso texto, mas antes, é imprescindível estudarmos mais alguns conceitos sobre a localização dos pontos no plano cartesiano. Nós vimos nos planos apresentados anteriormente, coordenadas dispostas por todos os seus quadrantes. Mas a verdade, é que podem existir pontos que se localizam exatamente sobre os eixos x e y, e também sobre as bissetrizes que cortam os quadrantes. Quando isso acontecer, as coordenadas terão uma configuração específica, olhem só!

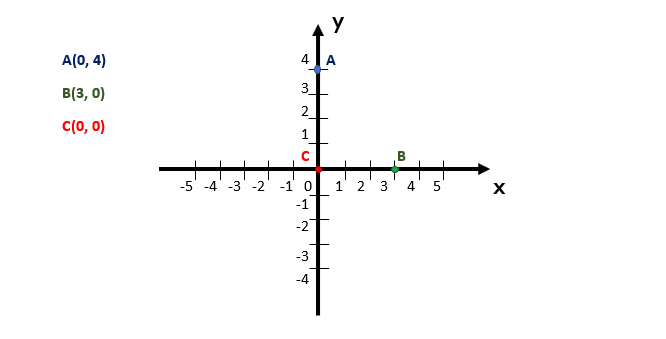
Qualquer ponto que se localize exatamente sobre o eixo das abscissas, sempre terá a configuração (x, 0). Isso significa que a coordenada x possuirá um certo valor real, enquanto a coordenada y certamente valerá zero. Um exemplo dessa situação é ponto B(3, 0), representado geometricamente no plano cartesiano acima.

Já quando um ponto qualquer se localiza exatamente sobre o eixo das ordenadas, ele certamente terá a configuração (0, y), o que significa que a coordenada y possuirá um certo valor real, enquanto a coordenada x valerá zero, com toda a certeza. O ponto A(0, 4), representado geometricamente no plano cartesiano acima, nos mostra um exemplo de uma situação como essa.

Assim, podemos concluir que o fato de um ponto se situar sobre um dos eixos cartesianos, implica em zerar a coordenada correspondente ao outro eixo. E aí eu pergunto: e se um ponto estiver localizado sobre os dois eixos, x e y? Só existe um lugar em que é possível fazer isso: na origem do plano cartesiano! É exatamente onde está localizado o ponto C da figura acima, sobre a origem do plano, e isso justifica porque as suas duas coordenadas foram zeradas!

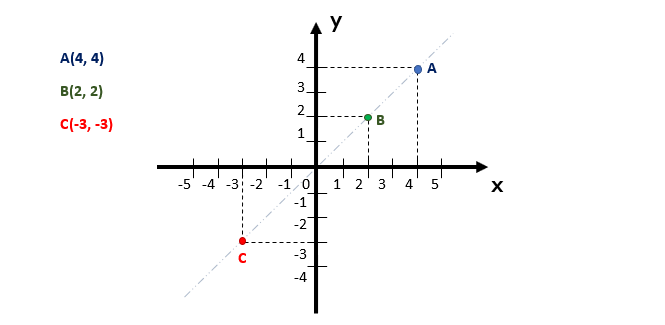
Agora vamos ver uma situação diferente. Vocês conseguiram notar algo em comum entre os pontos A, B, e C do plano cartesiano acima? Então olhem com bastante atenção: a verdade, é que todos eles possuem os valores das coordenadas x e y iguais! Isso sempre acontecerá quando os pontos forem localizados exatamente sobre a bissetriz dos quadrantes ímpares, que nós quase não conseguimos enxergar no plano acima. Assim, um ponto qualquer que se localiza exatamente sobre a bissetriz dos quadrantes ímpares, sempre terá a configuração (k, k), em que abscissa e ordenada possuem o mesmo valor.

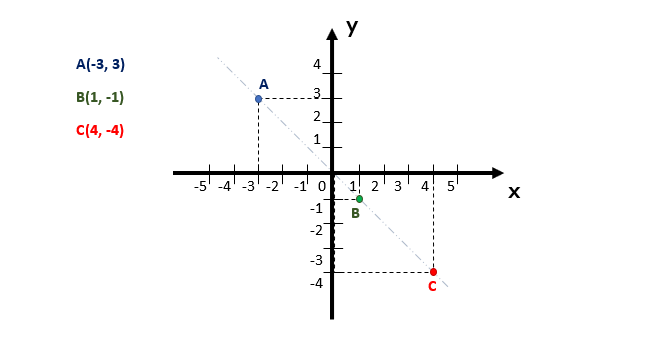
E se tratando da bissetriz dos quadrantes pares, o que será que acontece? Bom, se um ponto se localizar exatamente sobre ela, então as suas coordenadas terão o mesmo valor em módulo, mas sinais opostos, como são as coordenadas dos pontos A, B e C representados geometricamente no plano cartesiano acima. Por isso, podemos dizer que um ponto qualquer que se localiza exatamente sobre a bissetriz dos quadrantes pares, sempre terá a configuração (k, –k) ou (-k, k).

Acho que já vimos bastante coisa por hoje, não é? É por esse motivo que encerraremos o texto por aqui! Espero que esse assunto tenha sido bastante proveitoso para os estudos de vocês, e que todos os conceitos vistos aqui sejam úteis quando vocês precisarem construir um gráfico, ou realizar qualquer outra aplicação do plano cartesiano! Em anexo, deixo um vídeo que possui uma abordagem diferente e complementar a tudo o que vimos!

Um abraço e bons estudos!