INTRODUÇÃO AOS LOGARITMOS

Olá pessoal! Tudo bem com vocês?

No texto de hoje, abordaremos um assunto da matemática do ensino médio que costuma nos assustar um pouquinho: os temidos logaritmos! Mas na verdade, o logaritmo é uma função matemática muito interessante, totalmente baseada na função exponencial, de forma que se prestarmos bastante atenção no seu conceito, conseguiremos resolver qualquer situação proposta nas provas do ENEM e de vestibulares!

E claro, se vocês quiserem saber tudo sobre os logaritmos e outros assuntos vistos no ensino médio, assinem a plataforma do Professor Ferretto! Ela oferece uma série de videoaulas super didáticas, exercícios do ENEM e de vestibulares resolvidos, simulados semanais e muito mais! Acessem o site e confiram as vantagens oferecidas!

Ansiosos para começar? Vamos vencer os logaritmos, iniciando com uma breve introdução do assunto. Vem comigo aqui!

No estudo das equações exponenciais, tratamos de casos em que podíamos reduzir as potências à mesma base. Vamos fazer um exemplo para vocês lembrarem de como resolvíamos casos como esses:

2^x = 8

2^x = 2³

x = 3

Como pode ser visto acima, a ideia aqui era fazer com que ambos os lados da igualdade tivessem potências de mesma base. Fatorando o número 8, nós descobríamos que 8 = 2³, então bastava que fizéssemos essa substituição na equação, para encontrar a igualdade que desejávamos. Assim, era possível cortar as bases e trabalhar apenas com os expoentes, para finalmente chegar ao resultado da questão.

Em questões como a desse exemplo, nós conseguíamos igualar as bases para trabalhar apenas com os expoentes. Mas nem sempre isso é possível. O que fazer então em uma situação como a seguinte?

2^x = 3

Pensem comigo. Se o x for exatamente igual a 1, então 2¹ = 2, ou seja, o resultado é menor do que o desejado, que é 3. Agora se o x for exatamente igual a 2, então 2² = 4, ou seja, teremos um resultado maior que o desejado dessa vez. Utilizando esse raciocínio, a gente consegue concluir que o x é um valor que está entre 1 e 2, exatamente como mostra a figura abaixo:

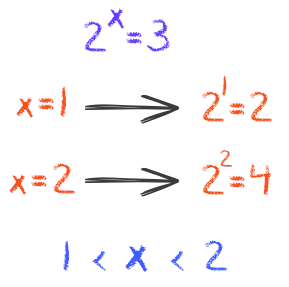
Então pessoal, reparem que nesse caso nós não conseguimos igualar as bases, somente chegamos à conclusão de que o valor de x está entre o 1 e o 2. Mas qual é exatamente esse valor entre 1 e 2? É aí que entra o Estudo dos Logaritmos! O logaritmo, dentre outras finalidades, ajuda muito a resolver esse tipo de equação onde não é possível igualar as bases das potências.

Preparados? Vamos iniciar agora o estudo dos logaritmos em si!

 

1. DEFINIÇÃO

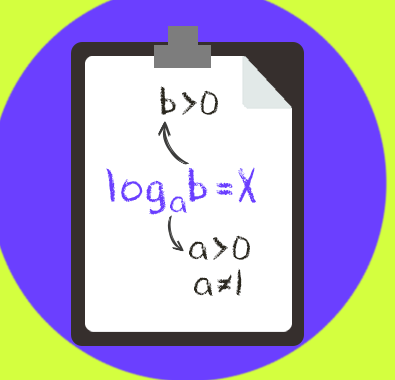
Sejam a e b números reais e positivos, com a ≠ 1, então:

Para entendermos direitinho essa definição, vamos imaginar duas retas reais, ou seja, duas retas que representam o conjunto dos números reais (ℝ), onde a primeira representará os valores de a, e a segunda representará os valores de b, como mostra a figura abaixo:

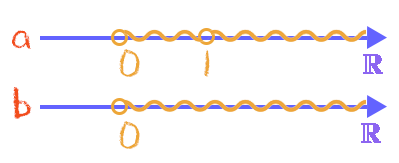
Reparem que a e b são números positivos, por isso devem ser maiores do que zero, mas nunca iguais a zero, afinal, o zero é um elemento neutro, e não um número positivo. Isso explica o fato de termos uma bolinha aberta no zero em ambas as retas reais, e também porque selecionamos toda a região que vai do zero ao mais infinito. Mas há ainda um último detalhe importante: a restrição no valor de a, que jamais poderá ser 1. Por isso, também colocamos uma bolinha aberta no valor 1 da reta real que corresponde aos valores de a.

Sabem por que prestar atenção nos valores de a e de b é tão importante? Porque se essas restrições que vimos acima não forem satisfeitas, os logaritmos não são definidos. Vou mostrar a vocês alguns exemplos de quando isso acontece.

log₃ (-27)

Observem que em relação ao valor de a, está tudo ok, não é? 3 é um valor maior que zero e diferente de 1. O problema aqui é o valor de b, -27, que está negativo. O valor de b deve ser sempre maior que zero ou positivo!

log₅ 0

Novamente, não temos problemas com o valor de a, que é 5. Mas vejam que aqui o valor de b é zero, e isso também não é permitido!

log₀ 3

Ao contrário dos exemplos anteriores, nesse caso o b vale 3, que é um valor maior que zero, então está tudo certo. Contudo, vejam que o nosso probleminha está no valor de a, que jamais pode ser zero!

log_-2 16

Novamente temos um valor de a que não é permitido. -2 é um número negativo, mas a deve ser sempre maior que zero e diferente de 1!

log₁ 7

Por fim, vejam que o nosso valor de a aqui é 1. Não haveriam problemas caso o valor de b fosse 1, mas a necessariamente deve ser diferente de 1!

Bem, acabamos de saber tudo sobre os valores possíveis de a e de b. Mas vocês sabem quem são esses termos, ou como são chamados? É isso que vamos ver em seguida.

 

2. NOMENCLATURA

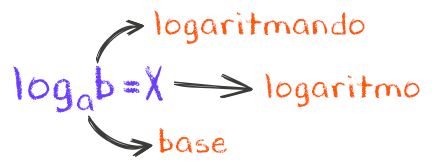
Então, o que vocês acharam da figura acima? Nela, podemos ver que o termo a, é conhecido como a base de um logaritmo, enquanto que o termo b é chamado de logaritmando. Um pouco estranho não é? Mas é isso mesmo! Já o termo x, o resultado de toda a operação, é o próprio logaritmo.

Pessoal, sempre tenham cuidado com as letras utilizadas para denominar esses três termos. Alguns livros colocam a letra b como sendo a base, o a como sendo o logaritmando, ou a letra m como sendo o logaritmando, enfim, mas isso não importa. O que precisamos entender é que a base é sempre aquele valor que está mais embaixo, e ela deve ser sempre positiva ou maior que zero, e diferente de 1. Já o logaritmando é um valor que está mais a frente, e deve ser sempre maior do que zero, ou positivo.

Assim, nós podemos fazer a leitura dessa operação da seguinte maneira: “O log ou o logaritmo de b, na base a, é igual a x”. Mas para resolvermos um logaritmo, utilizamos a operação chamada de logaritmação, que vou apresentar a vocês agora.

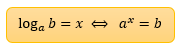
Na operação acima, nós observamos dois termos: o log_a b = x, de um lado, e o a^x = b no outro. Bom, eles estão separados por uma seta que aponta para ambos os lados. Essa seta está ali para nos informar que a expressão log_a b = x pode se transformar na expressão a^x = b, e vice-versa. Parece simples não é, mas como realizar essa transformação? É o que mostra a figura abaixo:

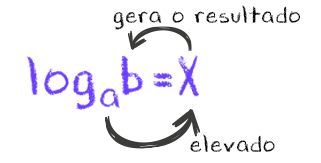
Vamos aplicar a logaritmação no exemplo que vimos no início da aula para tornar tudo mais claro:

Log₂ 3 = x

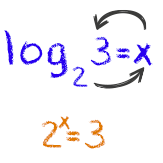
Simples não é? É só lembrar sempre: a nossa base terá o próprio logaritmo como seu expoente, e o resultado será o logaritmando!

Agora já sabemos quase tudo sobre os logaritmos! Resta-nos conhecer dois tipos de logaritmos muito utilizados, e que podem facilitar bastante os nossos cálculos.

 

3. SISTEMA DE LOGARITMOS DECIMAIS

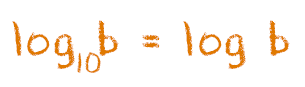
Um logaritmo decimal é aquele cuja base vale 10. Quando representamos um logaritmo como esse, podemos omitir o valor de sua base. Vejam só os exemplos abaixo:

log₁₀ 2 = log 2

log 5 = log₁₀ 5

 

4. SISTEMA DE LOGARITMOS NEPERIANOS

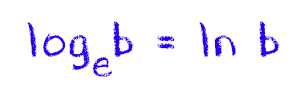
Os logaritmos neperianos são assim chamados em homenagem a uma matemático escocês, de nome John Napier, que foi o primeiro matemático a publicar um trabalho sobre logaritmos. Esse logaritmo possui como base o número de Euler, o e, cujo valor é um número irracional (e = 2,71828….). O número de Euler é muito conhecido, porque quando aplicado como base de uma função exponencial, consegue descrever diversos fenômenos naturais, e isso explica o fato desse logaritmo ser chamado também de logaritmo natural.

Assim, quando encontrarmos um logaritmo de base e, podemos reescrevê-lo omitindo a sua base, e substituindo log por ln, que faz referência a logaritmo natural. Olhem só como fica nesse exemplo:

log_e 5 = In 5

Vocês perceberão, ao longo do estudo, que é muito mais comum encontrarmos logaritmos decimais representados na forma “log x”, ou seja, quando o valor da base é omitido. Da mesma maneira, os logaritmos neperianos ou naturais costumam ser mais representados na forma “ln x”.

 

Chegamos ao final de mais um texto! Espero que os logaritmos não sejam mais tão temidos por vocês, e que conhecimento sobre o assunto agora, seja ainda maior! Deixo em anexo um vídeo, com a revisão de tudo que aprendemos hoje!

Um abração, bons estudos e até o próximo texto!