ESTUDO DO DOMÍNIO DAS FUNÇÕES REAIS

Olá, pessoal! Como vão vocês?

Estudar o domínio das funções reais, significa basicamente obter os valores de x que fazem com que essas funções existam! Sim, porque em determinadas situações, existem as chamadas impossibilidades matemáticas, e é delas que nós vamos aprender a fugir hoje! Para atingir esse objetivo, nada melhor do que resolver uma série de exercícios, não é mesmo? Portanto, se vocês são estudantes do ensino médio, ou pretendem realizar as provas do ENEM e dos vestibulares logo mais, não percam a oportunidade de complementar seus conhecimentos com os exemplos que vamos mostrar aqui!

Falando em exemplos, vocês sabiam que na plataforma do Professor Ferretto tem mais de 1000 exercícios do ENEM e de vestibulares resolvidos em vídeo? Nesses exercícios, procuro sempre trabalhar com foco na interpretação das questões, algo de extrema importância nos dias de hoje. E olha que isso é só uma pequena parte do que plataforma pode lhes oferecer: são videoaulas, simulados, planos de estudo, estatísticas individuais e muito mais! Acessem o site e saibam como ser alunos do Professor Ferretto!

Beleza, pessoal? Pois bem, quando falamos de uma função, é muito importante termos em mente 3 componentes essenciais a ela: o seu domínio, ou conjunto de partida, o seu contradomínio, ou conjunto de chegada, e também a própria lei de correspondência dessa função, que relaciona ambos os conjuntos.

Quando é citada uma função f de A em B, já ficam subentendidos o domínio (A) e o contradomínio (B).

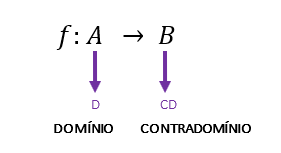
Geralmente, todos esses componentes são apresentados nos enunciados dos exercícios, ou então nas definições das mais variadas funções. Um exemplo disso é o caso da definição da função afim:

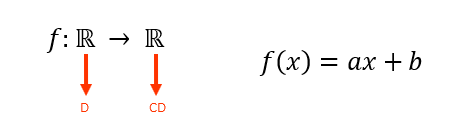
Vejam que a lei de correspondência da função afim é f(x) = ax + b, e que ela é dita como f: ℝ ⟶ ℝ. Isso significa que tanto o seu domínio, quanto o seu contradomínio, são formados pelo conjunto dos números reais. Agora, o fato é que muitas vezes nos é informada apenas a lei de correspondência de determinada função, mas não a regra que disponibiliza o seu domínio e o seu contradomínio, como essa que acabamos de ver. Sem essa regra, como poderíamos determinar o domínio e o contradomínio das funções abaixo, por exemplo?

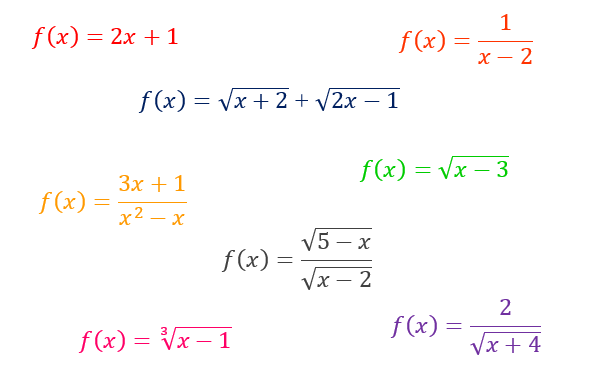
E aí, alguma ideia? Pessoal, nós começaremos sempre afirmando que o contradomínio de qualquer função real é formado pelo conjunto dos números reais. Tendo isso vista, e sabendo que quando os valores do domínio são aplicados na lei de correspondência de uma função, eles geram como resultado valores presentes no contradomínio dessa mesma função, podemos dizer que os valores do domínio, quando aplicados a uma função real, devem resultar em números reais. É aí que mora o segredo da questão:

Uma função existe, quando cada elemento do seu domínio resulta em um único elemento do seu contradomínio.

 

Pessoal, se a questão de domínio e contradomínio ainda é confusa para vocês, eu peço, não se assustem! Na prática, devido as condições que adotamos para o contradomínio das funções reais, nós podemos afirmar que o domínio de uma função real, é formado por todos os valores reais que podem assumir o lugar de x de tal maneira que essa função exista, ou seja, que ela resulte em valores também reais!

Aí que está, pessoal, nem sempre! Tudo vai depender das características da função, como vocês podem ver nos exemplos abaixo:

Vejam, – 4 e 0 são números reais. Só que devido as características das funções acima, quando esses valores são inseridos no lugar de x, as funções não resultam em um valor real. Nesse caso, diz-se que essas funções não existem para tais valores de x! Por isso, lembrem sempre: não existem resultados reais para radicais de índice par cujo radicando é negativo, e muito menos para divisões por zero!

Assim, nosso trabalho daqui pra frente será analisar uma série de funções, determinando para quais valores de x elas existem, ou seja, resultam em um valor real. Quando encontrarmos valores de x que não permitem isso, nós os descartaremos do domínio da função. Vamos começar? Então, vem comigo aqui!

 

Observem que podemos substituir o valor de x dessa função por qualquer valor real, e ela irá resultar em outro valor real também. Em casos como esse, diz-se que não há restrição alguma quanto ao domínio da função, e por isso ele é formado pelo conjunto dos números reais.

 

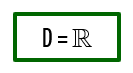
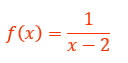
Opa! Esse é um caso em que podemos encontrar algum problema! Vejam, nós temos uma função cuja variável encontra-se no denominador de uma fração, mas nós sabemos que o denominador de qualquer fração jamais pode ser zero. Por isso, o domínio dessa função será formado por todos os valores reais que podem substituir o lugar de x, de forma que o denominador da função seja diferente de zero:

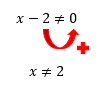
A resolução da inequação acima, nos mostra que 2 é o único valor que quando substitui o lugar de x, faz com que a função não resulte em um valor real, mas sim em um valor indefinido, dado por uma divisão por zero. Por isso, devemos excluir o número 2 do domínio da função f(x), o que é apresentado na sequência, primeiro em forma de propriedade, e em seguida em forma de intervalo, onde o número 2 é apresentado como um conjunto unitário.

 

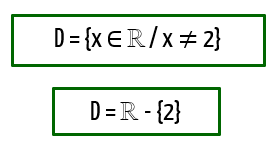
Hummm, e agora surgiu uma função composta por uma raiz quadrada! Uma raiz quadrada possui índice 2, que é par, e por isso não pode conter um radicando negativo. Então, qualquer número que seja maior ou igual a zero, pode pertencer ao radicando dessa função:

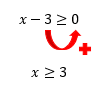
Assim, podemos concluir que qualquer número real maior ou igual a 3, quando substitui o lugar de x na função, faz com que a mesma resulte em um valor também real. Isso significa que somente esses valores fazem parte do domínio da função f(x).

 

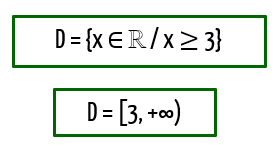
E agora, que temos uma função composta por uma raiz cúbica, será que muda alguma coisa? É claro que sim! A raiz cúbica é um radical de índice ímpar, e por isso o valor presente em seu radicando pode ser qualquer número real, incluindo os números negativos. Nesse caso, qualquer valor real que substitua x fará com que a função resulte em valores também reais. Aí, só podemos concluir que:

 

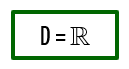
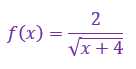
Nesta nova função f(x), nós teremos dois possíveis problemas no denominador. Primeiro, o denominador de qualquer fração jamais pode ser zero, e é claro que isso continua válido por aqui. Segundo, é que nesse caso em especial, o denominador é composto por uma raiz quadrada, cujo índice é par! Tendo isso em vista, é possível afirmarmos que o radicando dessa raiz não pode ser de forma alguma um valor igual a zero, ou negativo!

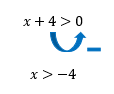
Assim, qualquer valor maior que –4, sem incluir o próprio –4, pode substituir o lugar de x, e então a função sempre resultará em valores reais!

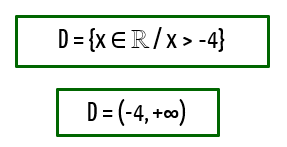
Pois bem, até então nós encaramos algumas situações bem simples de estudo do domínio de uma função real. Contudo, é chegada a hora em que deveremos tomar decisões um pouquinho mais exigentes. Vamos estudar agora, o domínio de funções em que duas sentenças precisam ser válidas. Quando isso acontece, vocês vão ver, é necessário realizar a intersecção dessas duas sentenças, e o resultado será formado por valores que atendem a ambas as partes. Querem ver como funciona? Então continuem comigo!

 

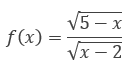
Vejam só, nesta função, tanto numerador quanto denominador são compostos por radicais de índice 2, um índice par. Por isso, é claro, ambos os radicandos não podem ser formados por números negativos. Agora, um detalhe não pode ser esquecido: o denominador de qualquer fração jamais pode ser zero! Então, por mais que para o numerador da função seja suficiente um valor maior ou igual a zero, para o denominador, apenas um valor positivo pode ser válido:

Valores maiores do que 2 satisfazem a sentença do denominador, embora somente valores menores ou iguais a 5 satisfaçam a sentença do numerador. Então, quais valores de x satisfazem ambas as sentenças? É o que nós veremos aqui através da interseção dessas duas análises:

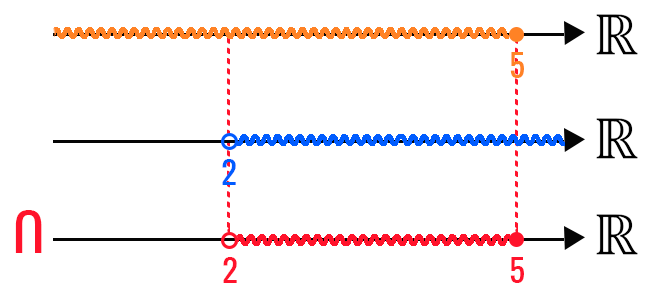
Ora, nesse caso, apenas valores de x que se situam entre 2 e 5, incluindo o número 5, fazem com que a função como um todo resulte em valores reais. Assim, podemos definir o domínio de f(x) das duas maneiras apresentadas abaixo:

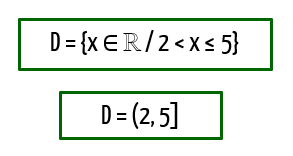
Tudo entendido, pessoal? Então, antes de prosseguirmos, aqui vai um aviso bem importante: se vocês não entenderam as resoluções das inequações do último exemplo, é imprescindível darem uma olhada no texto Introdução à inequação do 1º grau. Lá vocês descobrem porque multiplicamos a primeira inequação por –1! E agora, vamos continuar…

 

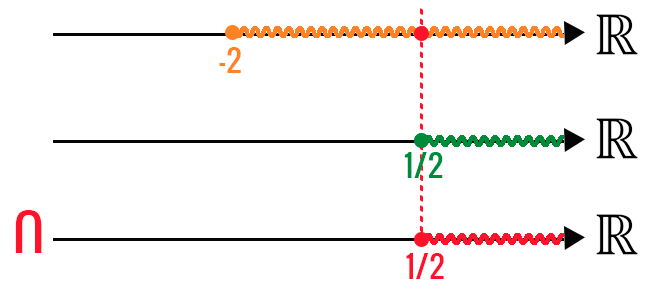
Apesar desta função não ser formada por uma fração, é fato que ela possui uma soma de dois radicais, cujo índice, é novamente par. Isso significa que em ambos os casos, o radicando deve ser um valor positivo ou igual a zero. Por isso, vamos resolver essas duas sentenças, e em seguida, realizaremos a intersecção das mesmas, afim de encontrar uma solução que satisfaça toda a função:

:

A intersecção dessas sentenças é importante, porque mostra que nem sempre os valores de x que ficam entre as mesmas são aqueles que satisfazem toda a função. Nesse caso, apenas valores maiores ou iguais a ½ fazem com que a função como um todo resulte em valores reais. Então, é claro que o domínio de f(x) só pode ser formado por esses valores:

 

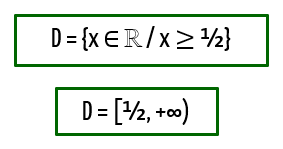
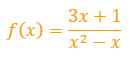
O nosso último exemplo também é um caso bem curioso. Apesar de possuirmos funções diferentes no numerador e no denominador da fração, o que poderia nos levar a uma intersecção, é fato que no numerador, qualquer valor que assuma o lugar de x faz com que a função resulte em valores reais. Por isso, precisamos apenas avaliar o denominador da função, porque este sim, jamais pode ser zero!

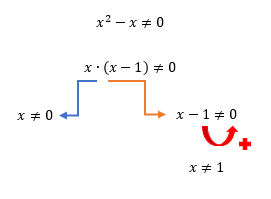
Pessoal, para quem não conhece, nós acabamos de analisar uma expressão do 2º grau incompleta. Em casos como esse, para simplificar a solução, nós costumamos colocar os termos comuns em evidência e trabalhar com o seguinte conceito: para que o produto entre dois termos seja diferente de zero, nenhum desses dois termos pode ser nulo, ou igual a zero. Para saber mais sobre o assunto, não deixem de ler o texto Equações do 2º Grau Incompletas!

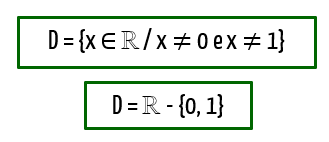
Sabendo que qualquer valor real, que não seja zero ou 1, pode ser substituído por x nessa última função de forma que ela resulte em valores reais, nós já podemos encerrar esse texto! Espero que tenham gostado do assunto, e que tudo o que vimos aqui contribua muito para desenvolvimento do raciocínio de vocês! É claro que em anexo fica aquele vídeo que complementa tudo o que vimos aqui. Não deixem de dar uma olhada nele, caso os conceitos de intersecção, intervalos ou qualquer outro fato relacionado ao assunto tenha soado um pouco confuso!

E eu, fico por aqui! Um abraço pessoal, e até o próximo texto!