PROPRIEDADES OPERATÓRIAS DOS LOGARITMOS
27/07/2018
Olá pessoal! Tudo certo?
É fato que a resolução da maioria dos logaritmos costuma ser complicada sem o uso de uma calculadora científica. O que fazer então quando aquelas expressões repletas de logaritmos aparecem nas provas de matemática do ENEM e dos vestibulares? É nesses momentos que precisamos usar algumas cartas na manga: as consequências da definição dos logaritmos e as suas propriedades operatórias! Vocês verão nesse texto, que quando o logaritmando de um logaritmo qualquer é formado por um produto, um quociente ou uma potência, é possível reescrever a expressão de uma maneira diferente, o que em alguns casos, pode ser crucial para a resolução de questões.
Mas não são só os logaritmos que contam com métodos alternativos que facilitam a resolução de exercícios. Para tudo há um caminho mais fácil, e quando se trata de matemática, esse caminho certamente se encontra na plataforma do Professor Ferretto! Todas as videoaulas e resoluções de exercícios do curso, são produzidas de forma didática, e com foco na interpretação, para que o aluno possa enfrentar as provas do ENEM e dos vestibulares encarando até mesmo as questões de matemática mais difíceis com tranquilidade! Se vocês não conhecem a plataforma, basta acessar o site para conferir todos os benefícios!
Então, sem mais delongas, é hora de iniciarmos nosso estudo! Mas antes de abordarmos as propriedades operatórias dos logaritmos em si, vamos relembrar rapidamente como um logaritmo é formado.
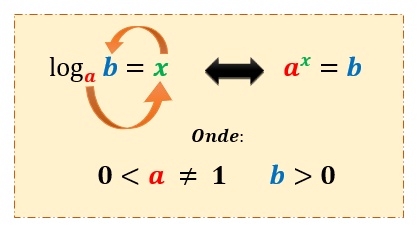
No quadro acima, é possível ver todos os termos que compõem um logaritmo: a é conhecido como sua base, enquanto o termos b e x são chamados, respectivamente, de logaritmando e logaritmo ou resultado da operação. O quadro também nos mostra que a logaritmação é a operação inversa da exponenciação, e isso justifica as restrições que os valores de a e b possuem. A base a deve ser sempre um valor maior que zero e diferente de 1, enquanto que o logaritmando b deve ser necessariamente um valor maior que zero, ou positivo.
Conhecendo esses detalhes, vocês entenderão direitinho as três propriedades que veremos a seguir!
1. LOGARITMO DO PRODUTO
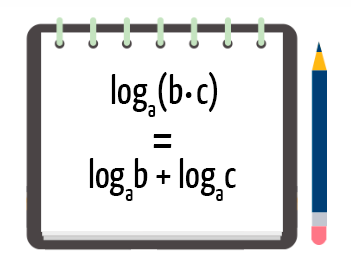
Numa mesma base a (a > 0 e a ≠ 1), o logaritmo do produto de dois números reais e positivos é igual a soma dos logaritmos desses números.
De acordo com essa propriedade, quando temos um único logaritmo de um produto entre dois números b e c, esses dois números b e c podem se separar em dois logaritmos distintos, cuja base será a mesma do logaritmo “original”. Ou seja, uma multiplicação em um mesmo logaritmo, pode se transformar em uma adição de dois logaritmos distintos.
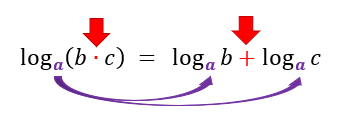
Aí é muito importante lembrarmos, que as restrições para a base a e para os logaritmandos b e c ainda estão valendo! a deve ser sempre um valor maior que zero e diferente de um, da mesma forma que o logaritmando deve ser sempre um valor positivo. É por isso que b e c são mencionados como dois números reais positivos (b > 0 e c > 0).
Abaixo, seguem dois exemplos numéricos do uso desta propriedade. Olhem só:
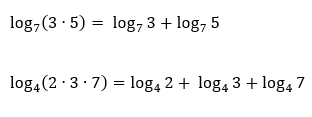
Observem no último exemplo, que esta propriedade não se restringe ao logaritmo do produto de apenas 2 termos. Ela pode ser utilizada para o produto de n termos, desde que ao aplicar a propriedade, o número de multiplicações seja convertido no mesmo número de adições de n logaritmos distintos.
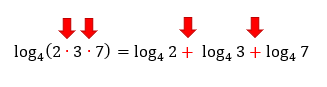

O tamanho do quadro acima faz referência ao tamanho do problema que vocês enfrentarão se adotarem como igual alguma das sentenças acima. Nós estudamos que uma multiplicação em um mesmo logaritmo, pode se transformar em uma adição de dois logaritmos distintos, mas não o contrário, como mostra a primeira sentença do quadro. Uma soma em um mesmo logaritmo não pode se transformar em um produto de dois logaritmos distintos, porque essas operações não resultam no mesmo valor. O que realmente é válido, é encontrarmos uma adição de dois logaritmos de mesma base, e transformarmos isso em um único logaritmo de um produto, o que é exatamente o processo inverso da propriedade que acabamos de aprender:
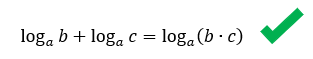
Já a segunda sentença apresentada no quadro, nos mostra o quão importante é a utilização dos parênteses em uma expressão matemática. Sem o uso deles, o produto entre dois termos no logaritmando não é garantido, e o que se tem, na verdade, é um valor numérico multiplicando o logaritmo como um todo. Por isso, quando houver qualquer valor numérico se relacionando apenas com o logaritmando de um logaritmo, não esqueçam de utilizar os parênteses! Contudo, se esse mesmo valor numérico estiver se relacionando com o logaritmo como um todo, seja através de uma adição, subtração, multiplicação, ou de qualquer outra operação, então é melhor seguir a dica de representação abaixo:

Assim, eu garanto, não haverá confusão alguma quanto aos termos que fazem parte do logaritmando dos mais diversos logaritmos. Agora, é hora de conferirmos mais uma propriedade!
2. LOGARITMO DO QUOCIENTE
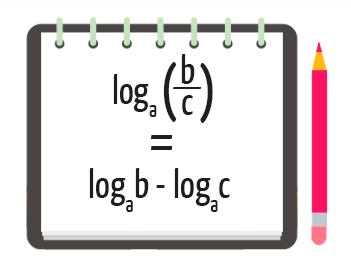
Numa mesma base a (a > 0 e a ≠ 1), o logaritmo do quociente de dois números reais e positivos é igual à diferença entre os logaritmos desses números.
De acordo com essa propriedade, quando temos um único logaritmo de um quociente, ou de uma divisão entre dois números b e c, esses dois números b e c podem se separar em dois logaritmos distintos, cuja base será a mesma do logaritmo “original”. Ou seja, uma divisão em um mesmo logaritmo, pode se transformar em uma subtração de dois logaritmos distintos.
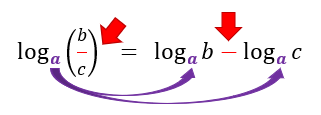
Da mesma forma que na propriedade anterior, as restrições para os valores da base a (a > 0 e a ≠ 1) e para os valores dos logaritmandos b e c (b > 0 e c > 0) permanecem valendo. E o mais interessante dessa propriedade, é que podemos utilizar a semelhança entre o sinal de divisão e o sinal de subtração para memorizar que uma divisão em um mesmo logaritmo gera uma subtração de dois logaritmos distintos. É claro que realizar o processo inverso da propriedade também é válido, mas transformar uma subtração em um mesmo logaritmo em uma divisão de dois logaritmos distintos é completamente incorreto!
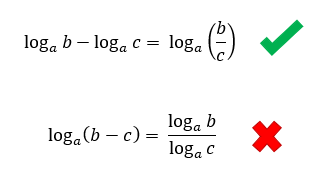
Abaixo, seguem alguns exemplos numéricos do uso desta propriedade. Olhem só:
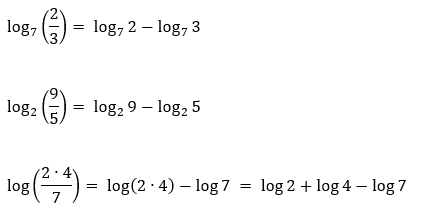
Vejam que no último exemplo, houve uma mistura das duas propriedades que nós já estudamos. Mas não há motivo para se preocupar com isso. Basta aplicarmos primeiro a propriedade do logaritmo do quociente, e em seguida aplicarmos a propriedade do logaritmo do produto ao termo que ficou com um produto, transformando-o assim, em uma soma de logaritmos distintos. Outro detalhe interessante, é que esse último logaritmo de que tratamos não apresenta base alguma. Isso significa que ele é um logaritmo decimal, e portanto, para todos os efeitos, sua base é de valor 10.
3. LOGARITMO DA POTÊNCIA
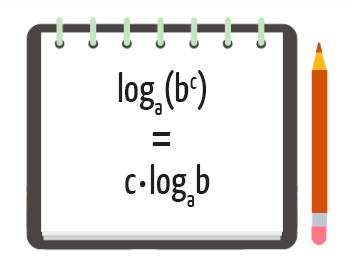
Numa mesma base a (a > 0 e a ≠ 1), o logaritmo da potência de base positiva é igual ao produto do expoente pelo logaritmo da base da potência.
Notem que esta propriedade é bastante diferente das anteriores, e por isso o seu conceito pode soar um pouco confuso. Mas fiquem tranquilos, a ideia é bem simples: quando o logaritmando de um logaritmo qualquer for composto por uma potência de base b e expoente c, é possível passar o expoente c dessa potência para frente do logaritmo, e então, c passará a multiplicar o logaritmo de b. É só pensar que o expoente da potência deve pular lá pra frente do logaritmo e multiplica-lo como um todo! E ainda temos a seguinte vantagem: a base a do logaritmo não sofre alteração alguma, como mostra a figura abaixo:
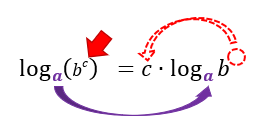
Se vocês repararem melhor, o conceito desta propriedade nos diz que a base b da potência deve ser positiva, ou maior do que zero (b > 0). Mas ao contrário das demais propriedades, nada é dito sobre c, o expoente da potência. O fato é que sendo a base b positiva, o logaritmando jamais será um valor negativo, independentemente do valor que c assumir. Por isso, na condição de expoente, c pode ser qualquer número real (c ∈ ℝ), ou seja, c pode ser positivo, negativo, fracionário, enfim, nessas condições, a existência do logaritmo é garantida!

E lá vem esse quadro enorme novamente! É que quando se fala em potenciação, também é bem importante o uso dos parênteses nas expressões. Vejam que no primeiro logaritmo apresentado, o expoente c pertence apenas a base b da potência, e portanto apenas ao logaritmando. Quando isso acontece é possível utilizar a propriedade que acabamos de estudar. Contudo, no segundo logaritmo apresentado, c é o expoente do logaritmo como um todo, fato que nos impede de aplicar a propriedade. As duas expressões não resultam no mesmo valor.
Agora, vamos aos famosos exemplos numéricos:
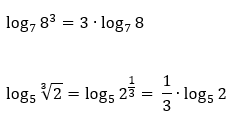
Vejam que no último exemplo, o logaritmando era composto por um radical. Mas felizmente, todo radical pode ser representado na forma de potência de expoente fracionário, através de uma das propriedades da potenciação. Bom, se há a formação de uma potência, então é claro que podemos aplicar a propriedade do logaritmo da potência, e assim, o expoente fracionário pula para a frente do logaritmo e o multiplica como um todo.
Certo, pessoal!? Essas propriedades realmente são muito importantes dentro do estudo dos logaritmos. Assim, espero que o estudo de hoje tenha sido bem proveitoso, e que vocês tenham entendido tudo direitinho para poder aplicar esse conhecimento com facilidade! Declaro que hoje não dá para deixar de ver o vídeo que está anexo! Lá vocês encontram uma série de exemplos resolvidos e ainda uma dica incrível para resolver logaritmos decimais!
Um abração! Voltamos a nos ver em breve!