PROPRIEDADES DO MÓDULO
20/06/2018
Olá pessoal! Tudo bem com vocês?
Hoje daremos mais um passo importante rumo ao estudo da função modular: investigaremos todas as propriedades do módulo! O módulo, é um assunto da matemática do ensino médio muito fascinante, porque apesar de parecer extremamente simples, pode causar aquela dúvida quando determinadas sentenças são analisadas. Aí está a importância de estudarmos as suas propriedades, afinal, conhecê-las direitinho é a garantia de sucesso nas provas de matemática do ENEM e dos vestibulares!
E caso vocês tenham muitas dúvidas no estudo do módulo, da análise combinatória, da trigonometria ou de qualquer outra área da matemática do ensino médio, é mais fácil de resolver do que parece: lhes apresento a Plataforma do Professor Ferretto! É uma plataforma moderna de estudo da matemática, onde vocês encontram videoaulas didáticas, materiais de estudo disponíveis para download, e ainda, no plano diamante, tem a disposição monitores treinados para sanar suas dúvidas em até 24h! Acessem o site e confiram todos os benefícios!
Para entendermos as propriedades do módulo, é essencial que conheçamos o conceito de módulo. Basicamente, o módulo ou valor absoluto de um número real x, que representamos por | x |, é definido através da seguinte relação:
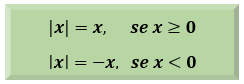
Aí vocês poderiam pensar: lá vem aquela linguagem matemática que a gente não entende nada. Pessoal, é muito simples! O quadro está nos mostrando que o módulo de qualquer número positivo e do número zero é igual a ele mesmo, enquanto que o módulo de qualquer número negativo é igual ao oposto dele mesmo. Olhem só esses dois exemplos:
| 5 | = 5
| – 9 | = – (– 9) = 9
No primeiro exemplo, como calculamos o módulo de um número positivo, o resultado foi o próprio número, 5. Já no segundo exemplo, calculamos o módulo de um número negativo, e como nesse caso, o resultado deve ser o oposto do número, basta multiplicarmos o valor, – 9, por “– 1”, e assim obtemos o seu oposto, 9. Portanto, podemos concluir que o resultado do módulo de qualquer número real jamais será um número negativo!
É imprescindível ter isso em mente para iniciarmos o estudo das propriedades do módulo. Vem comigo aqui!

Para todo x ∈ ℝ, temos | x | = | –x |.
Nós acabamos de aprender que o módulo de um número positivo é igual a ele mesmo, e que o módulo de um número negativo é igual ao oposto dele mesmo, gerando assim um resultado positivo também. Por isso, o módulo de um certo número x é exatamente igual ao módulo do seu oposto –x. Vamos fazer um exemplo numérico para que essa propriedade fique bem clara:
| 3 | = | –3 |
3 = – (– 3)
3 = 3

Para todo x ∈ ℝ, temos | x2 | = | x |2 = x2.
Essa propriedade normalmente é aplicada nas equações modulares. O fato, é que não importa se um certo valor x for elevado ao quadrado e do resultado for extraído o seu módulo, ou se for extraído o módulo de um certo valor x e só depois o resultado for elevado ao quadrado, ou mesmo se não existir a operação do módulo, e somente o valor x for elevado ao quadrado. Em todos esses casos, o resultado será igual. Querem ver como é verdade?
Para x = 5.
| x2 | = | 52 | = | 25 | = 25
| x |2 = | 5 |2 = 52 = 25
x2 = 52 = 25
Vejam que desenvolvemos direitinho cada uma das operações, e o resultado foi exatamente o mesmo para todas elas. Aí poderíamos pensar: mas e se x for negativo, será que dá certo? A resposta é que sim, dá certo, porque o quadrado de qualquer número real é sempre um valor positivo.
Para x = –3.
| x2 | = | (–3)2 | = | 9 | = 9
| x |2 = | –3 |2 = 32 = 9
x2 = (–3)2 = 9
Assim, acabamos de comprovar que a propriedade realmente é válida para todo x ∈ ℝ.

Para todo x ∈ ℝ, temos √(x2) = | x |.
Às vezes, por pura simplicidade, quando resolvemos uma raiz quadrada de um número elevado ao quadrado, optamos por cancelar o índice 2, da raiz quadrada, com o expoente 2 do número em questão. Nada de mal até aí, desde que consideremos que o resultado dessa operação seja o módulo de tal número, e não apenas o número.

Entenderam o porquê disto? Vou mostrar para vocês agora dois exemplos que tornam a questão muito clara:

No primeiro exemplo, onde calculamos a raiz quadrada de um número positivo elevado ao quadrado, parece que não houve problema quanto a considerar o resultado sem a aplicação do módulo. Contudo, quando calculamos a raiz quadrada de um número negativo elevado ao quadrado, no segundo exemplo, não foi possível obter respostas semelhantes. É aí que está o problema. Segundo a definição, a raiz quadrada de um número x é um número único e não negativo que, quando multiplicado por si próprio, se iguala a x. Por isso, na resolução usual, nós obtemos apenas valores positivos como resposta, e por isso também, que precisamos aplicar o módulo ao radicando quando efetuamos aquela simplificação do expoente com o índice da raiz!

Pessoal, é tão comum inserirmos o sinal ± na resolução de uma equação do segundo grau, que muitos de nós nem sabem ao certo porque isso é feito. Vou explicar direitinho para vocês agora: o sinal ± tem tudo a ver com a observação que estamos estudando. Acompanhem o exemplo abaixo.
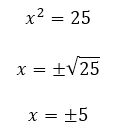
Isso é o que nós faríamos normalmente, certo? Mas o fato, é que para resolver uma equação como essa, devemos inserir uma raiz quadrada em ambos os lados da equação, olhem só:
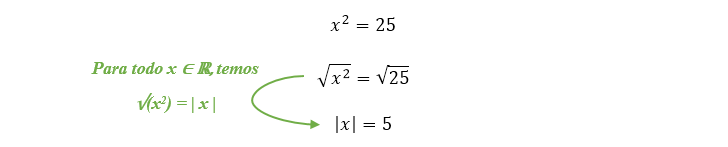
É aí que precisamos prestar bastante atenção! O sinal ± não irá aparecer porque a raiz quadrada de 25 pode ser +5 ou –5. A raiz quadrada de 25 é apenas +5! O fato é que tanto o módulo de 5 quanto o módulo de –5 geram o resultado 5. Estamos estudando aqui, o valor de x a partir do módulo de x.
| 5 | = 5
| –5 | = 5
Assim, o conjunto solução desta equação é dado por:
S = {–5, 5}
O mesmo acontece em um caso como esse:
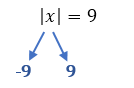
Tanto o módulo de 9, quanto o módulo de –9, resulta no valor 9. Por isso, as soluções que satisfazem este exemplo são dadas no conjunto abaixo:
S = {–9, 9}
Entenderam a ideia? É por esse motivo que costumamos usar o sinal ± naquele contexto de equação do segundo grau, porque o conceito de módulo está camuflado ali! Portanto, não esqueçam: a operação da raiz quadrada em si, resulta sempre em um único número positivo!
Agora, antes de estudarmos a próxima propriedade, vamos observar rapidamente mais um exemplo onde devemos buscar o valor de x a partir do módulo de x.
| x | = –2
Estranho não é mesmo, afinal estamos acostumados com essa situação:
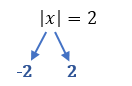
Tanto o módulo de –2, quanto o módulo de 2, resultam no valor 2, positivo. Mas não há valor algum de x, de tal maneira que o módulo de x seja –2. Portanto, pessoal, a solução para um caso como esse, em que se afirma que o módulo de um certo valor x deve resultar em um valor negativo, é sempre o conjunto vazio.
S = { }

Para todo x e y pertencentes a ℝ, temos | x ∙ y | = | x | ∙ | y |.
Em uma situação em que se busca o módulo do produto entre dois termos x e y, é indiferente calcularmos o produto entre os termos primeiro, e em seguida obtermos o módulo do resultado, ou então, calcularmos o módulo de cada termo separadamente para depois efetuar o produto dos resultados. Acompanhem o exemplo abaixo:
Para x = 3 e y = –2.
| x ∙ y | = | x | ∙ | y |
| 3 ∙ (–2) | = | 3 | ∙ | –2 |
| – 6 | = 3 ∙ 2
6 = 6
Vejam que independente da forma como resolvemos o caso, um resultado foi igual ao outro, por isso é possível “separar” os termos sem consequência alguma. Infelizmente, na próxima propriedade que veremos, não será possível afirmar o mesmo. Vem comigo aqui!

Para todo x e y pertencentes a ℝ, temos | x + y | ≤ | x | + | y |.
Quando se trata do módulo da soma entre dois termos x e y, separar os termos, efetuar o módulo de cada um deles, e só depois somar os resultados, pode resultar em um valor maior ou igual ao que se chega quando a soma entre os fatores é realizada por primeiro, e só do resultado dela é que se extrai o módulo. Vamos ver agora, através de exemplos, em que casos o resultado não é alterado e em que casos o resultado poderá ser maior.
Para x = 5 e y = 4.
| x + y | = | x |+ | y |
| 5 + 4 | = | 5 |+ | 4 |
| 9 | = 5 + 4
9 = 9
Nesse caso, o cálculo foi realizado apenas com valores de mesmo sinal, e sempre que isso acontecer o resultado irá se manter. Reparem agora na situação seguinte:
Para x = –3 e y = 2.
| x + y | < | x |+ | y |
| –3 + 2 | < | –3 |+ | 2 |
| -1 | < 3 + 2
1 < 5
Se os valores x e y possuem sinais diferentes, quando a soma é realizada primeiro, acontece na verdade uma subtração, diferente do caso em que o módulo é extraído primeiro, já que assim, os resultados são apenas positivos, e desta forma, jamais uma subtração seria realizada. Por isso, um valor acaba sendo maior que o outro.
Assim podemos concluir brevemente, que quando houver um caso de módulo da multiplicação entre dois termos, não há problema algum em separar os fatores. Contudo, quando se tratar do módulo da soma entre dois termos, nem sempre é possível separar os fatores, então temos que ficar bem atentos as diferentes aplicações desta propriedade.
Certo, pessoal? Encerro o texto de hoje ainda mais encantado pela matemática, e espero ter contagiado todos vocês! Tenham certeza de que todo o conhecimento disponível aqui vai lhes ajudar a ir longe e alcançar tudo o que almejam! Só não deixem de olhar o vídeo que trago em anexo. Nele, vocês encontram exercícios resolvidos sobre o assunto, e uma abordagem que complementa tudo que foi visto!
Um forte abraço e até o próximo texto!