A diferença entre dois conjuntos A e B, é um conjunto formado pelos elementos de A que não pertencem a B. Em outras palavras, pode-se dizer que essa diferença é dada pelos elementos que pertencem exclusivamente a A, quando comparados com os elementos de B.

 

Olá, pessoal! Como vão?

É verdade que no cotidiano nós costumamos utilizar muito a subtração, que é, inclusive, uma das quatro operações fundamentais da aritmética. Agora, vocês já pensaram algum dia em aplicar essa operação na teoria dos conjuntos? Pois então, saibam que é possível calcular a diferença entre dois conjuntos!

Neste texto, nós vamos entender direitinho o cálculo que envolve essa operação. Faremos também alguns exemplos, de modo a consolidar esse conhecimento. Mas para entendermos com clareza todos os conceitos que serão vistos logo mais, iniciaremos os estudos com uma breve revisão. Ela abordará a forma como dois conjuntos A e B se relacionam quando possuem, ou não, elementos em comum. Vem comigo!

 

1. REVISANDO A TEORIA DOS CONJUNTOS

Quando se fala em teoria de conjuntos, a representação na forma de diagrama torna a resolução das operações muito mais simples. Bom, pelo menos é o que acontece na maioria das vezes. Por isso, vamos revisar agora 3 maneiras nas quais dois conjuntos A e B podem se relacionar juntamente a sua representação na forma de diagrama. Acompanhem comigo.

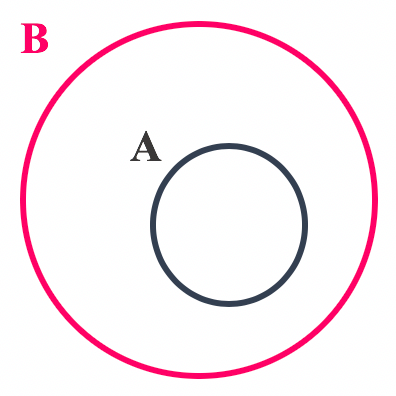
Quando A é subconjunto de B, pode-se dizer que A é parte de B, ou que A está contido em B. Isso significa que todos os elementos de A também pertencem ao conjunto B.

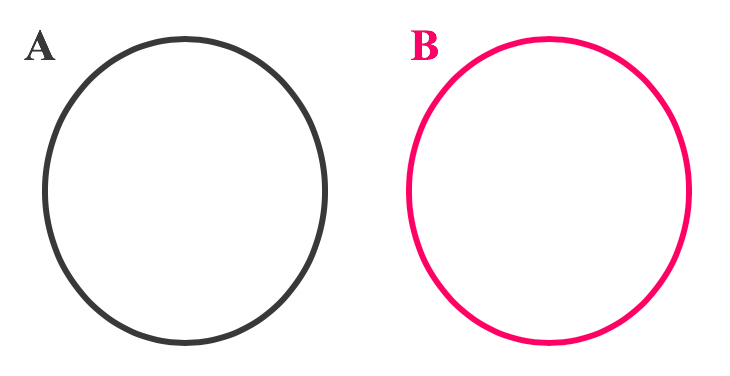
Já quando A e B são conjuntos disjuntos, significa que eles não possuem elementos em comum, ou seja, é um caso em que nenhum elemento de A também pertence a B, e vice-versa.

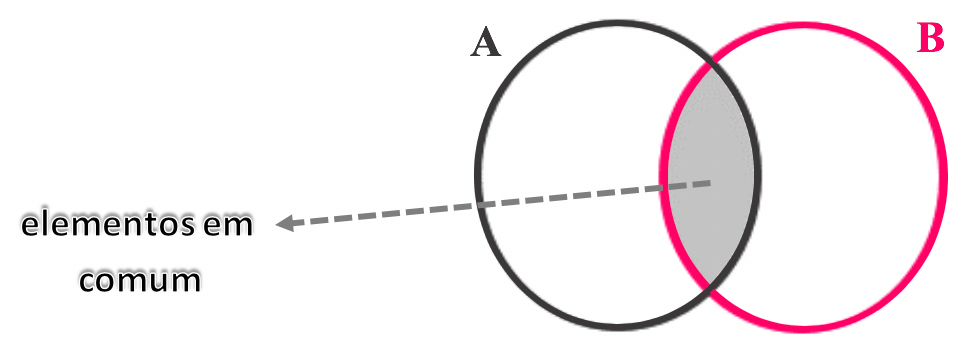
E por fim, quando os diagramas de A e B estão entrelaçados, significa que estes dois conjuntos possuem apenas alguns elementos em comum.

Entendido, pessoal? Sendo assim, podemos partir com tranquilidade para operação entre conjuntos que aprenderemos hoje. Sigam comigo!

 

2. DIFERENÇA ENTRE DOIS CONJUNTOS

Dados dois conjuntos A e B, chama-se diferença entre A e B, o conjunto formado pelos elementos de A que não pertencem a B.

Em outras palavras, podemos dizer que os elementos que estão no conjunto A, e não fazem parte do conjunto B, formam o conjunto diferença entre A e B (A – B). Já em forma de símbolos, a diferença entre os conjuntos A e B é dada pelo conjunto dos elementos x, tais que esses elementos x pertençam ao conjunto A mas não pertençam ao conjunto B. É isso que aparece no quadro abaixo.

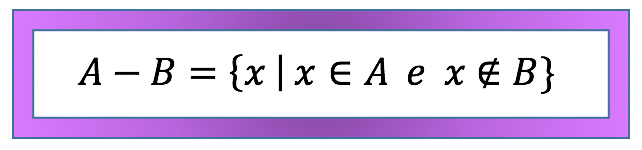
E aí, o que acharam desta definição? Quando olhamos para o exemplo que o nosso amigo apresenta no quadro, as coisas começam a ficar um pouco mais claras, não é? É por isso que partiremos agora para os famosos exemplos resolvidos! Eles nos possibilitarão enxergar o assunto através de mais alguns pontos de vista. Vem comigo!

 

2.1 Exemplos resolvidos sobre a diferença entre dois conjuntos

 

1. Em todos os itens, obtenha o conjunto diferença entre A e B (A – B). Em seguida, encontre também o conjunto diferença entre B e A (B – A).

a. A = {1, 2, 3, 4} e B = {2, 4, 5}

Acabamos de aprender que o conjunto diferença entre A e B é formado pelos elementos que pertencem a A e não pertencem a B. Baseando-se nessa ideia, vocês sabem como resolver essa questão? Fiquem tranquilos, pessoal, a ideia é comparar tudo com a subtração mesmo, como dissemos lá no início do texto. Para conhecer os elementos do conjunto A – B, basta observamos os elementos que pertencem a ambos os conjuntos, e descontá-los, tirá-los, ou riscá-los do conjunto A. Os elementos que restarem formarão o conjunto diferença que tanto buscamos. Vejam só:

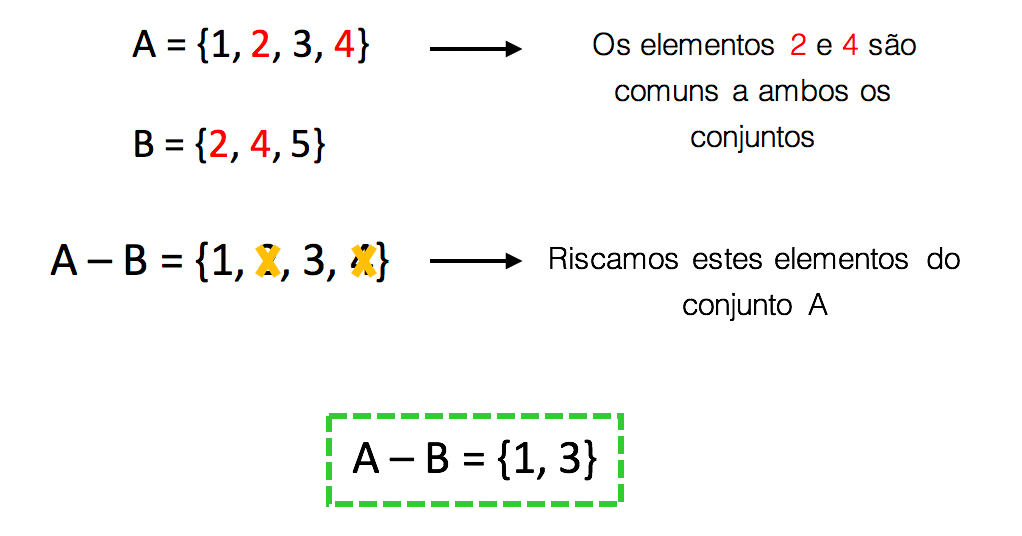
Observem que nós literalmente riscamos os elementos que são comuns a ambos os conjuntos. Isso aconteceu porque deveríamos descontar dos elementos de A, todos os elementos que também pertenciam a B. Notem que o conjunto resultante A – B foi formado pelos elementos que pertencem exclusivamente a A.

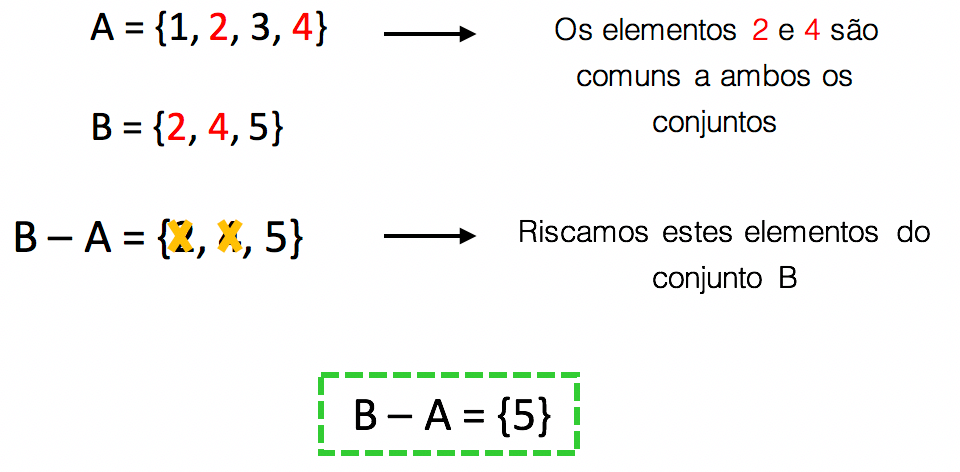
É claro que para obter o conjunto diferença entre B e A, a lógica precisa ser invertida. Vamos observar novamente os elementos que são comuns a ambos os conjuntos, mas agora vamos riscá-los de B, porque queremos descontar dos elementos de B, todos os elementos que também pertencem a A. Assim, B – A será formado apenas pelos elementos que pertencem exclusivamente a B.

 

Facilitando a operação entre os conjuntos com a representação na forma de diagrama

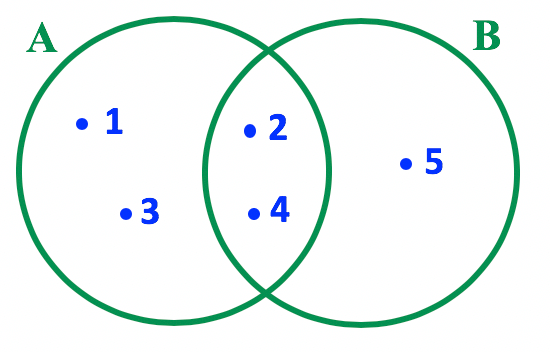
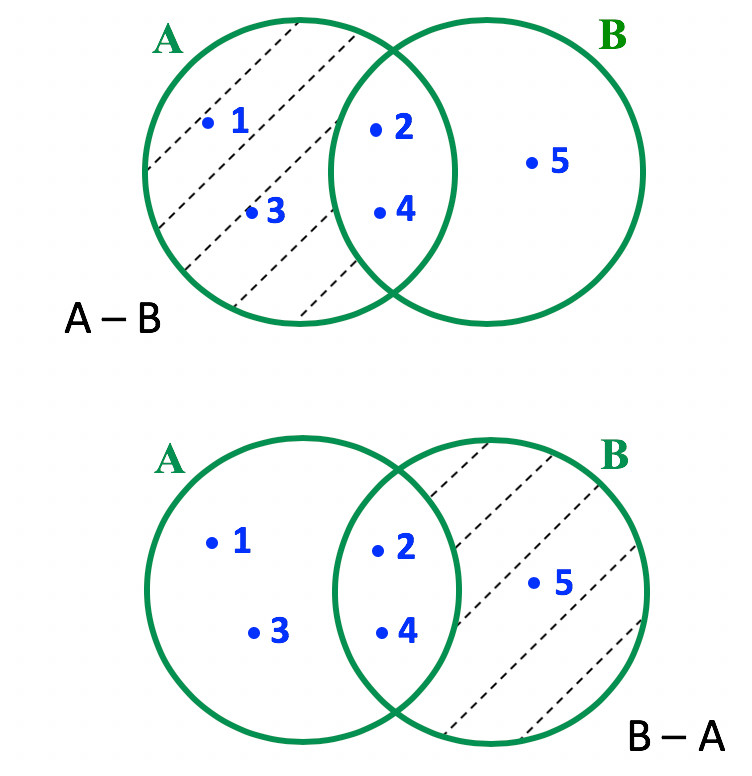
Através do diagrama fica ainda mais fácil de compreender a diferença entre os conjuntos A e B, e B e A. No primeiro caso, A – B, estamos descontando ou retirando B. Portanto, basta desconsiderar toda a região dos elementos que pertencem a B. Já no segundo caso, B – A, vejam que quem está sendo subtraído, ou excluído, é o A. Assim, é só desconsiderar toda a região dos elementos que pertencem a A, como mostra a imagem seguinte.

 

b. A = {a, b, c} e B = {d, e}

Agora que já sabemos exatamente o que fazer, podemos determinar os conjuntos A – B e B – A sem rodeios. Mas vejam só que coisa interessante: nesse caso, A e B não possuem elementos em comum, ou seja, eles são conjuntos disjuntos.

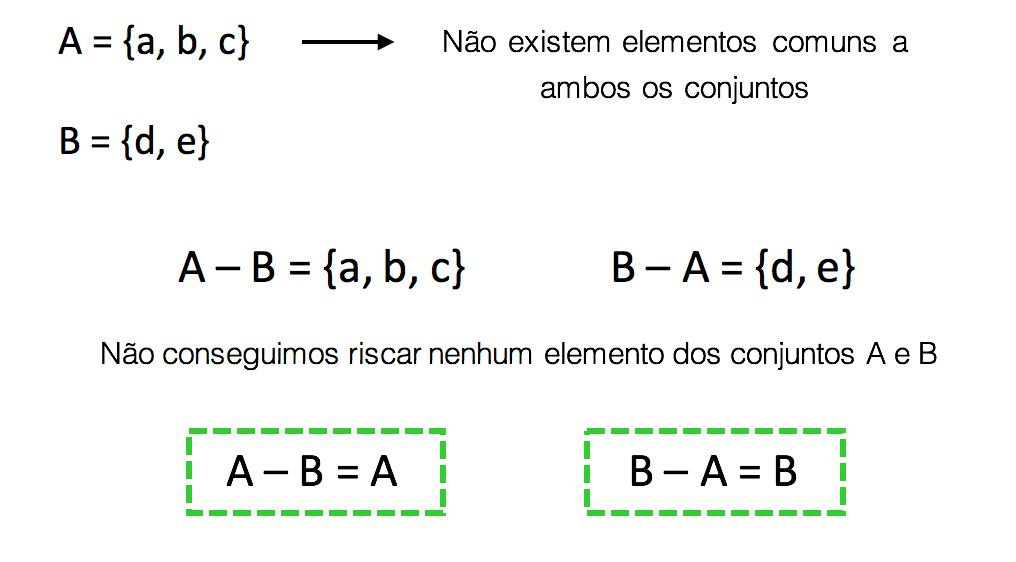
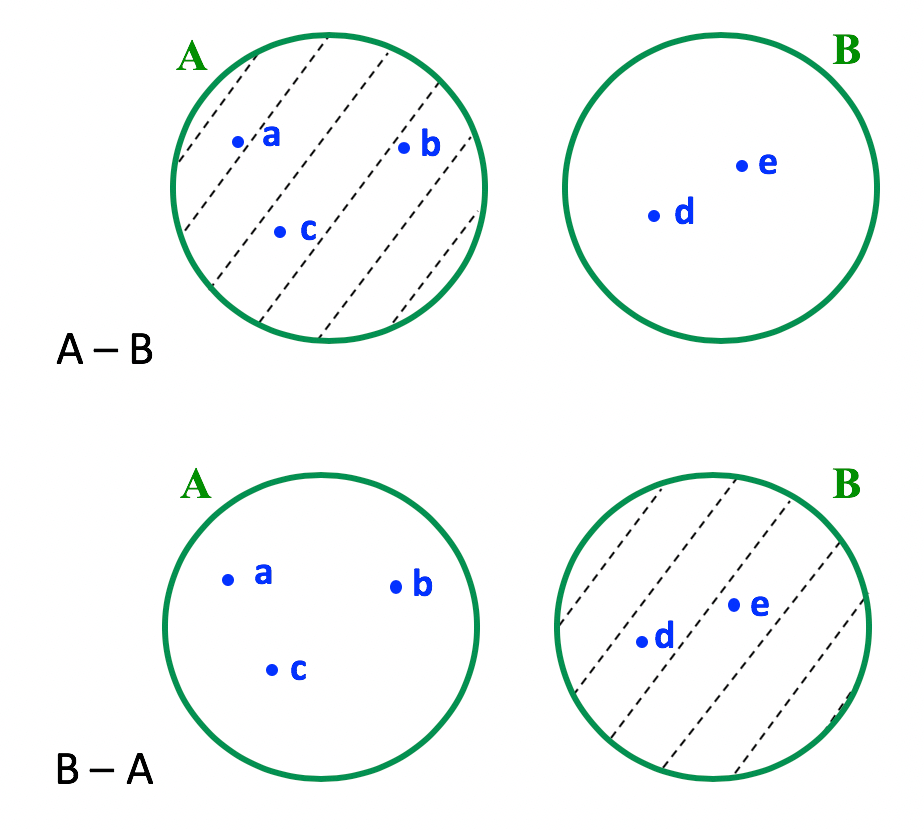
Podemos entender melhor o caso quando nos perguntamos: o que acontece quando descontamos ou subtraímos o número zero de qualquer número real? Não há mudança alguma, não é mesmo? Bom, se A e B são disjuntos, existem zero elementos comuns entre eles, ou seja, todos os elementos pertencentes a A já são exclusivos de A. Da mesma forma, os elementos de B também já são exclusivos de B. Por isso, não conseguimos riscar elemento algum nos dois cálculos. Assim, é possível concluir que a diferença entre A e B é o próprio conjunto A, enquanto que a diferença entre B e A é o próprio conjunto B.

 

c. A = {a, b} e B = {a, b, c}

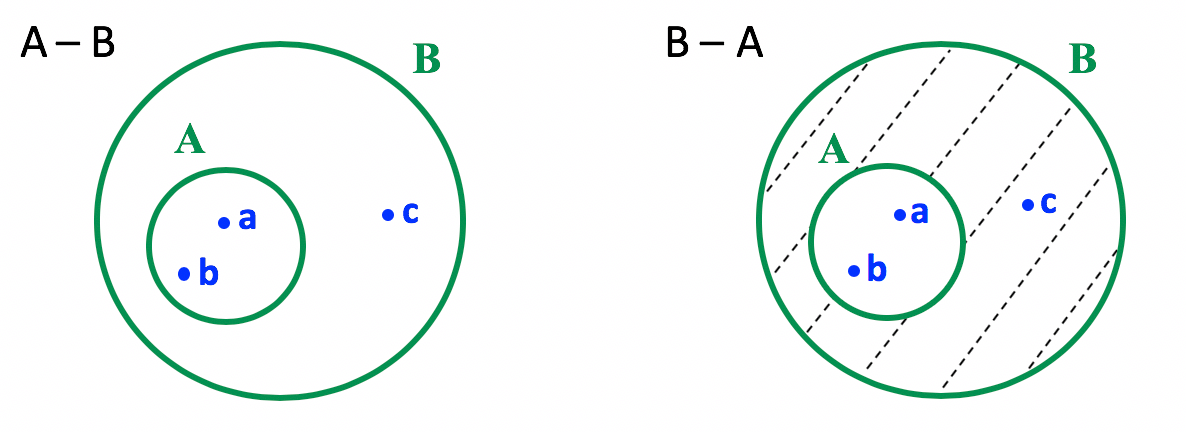
Quem prestou atenção na revisão logo no início do texto, já percebeu que nesse item A é subconjunto de B, pois todos os seus elementos também pertencem a B. Calculando os conjuntos diferença entre A e B e B e A, veremos em que situação curiosa isso vai dar. Vem comigo!

 

Quando A é subconjunto de B

Quanto ao conjunto diferença entre B e A, tudo certo, não é mesmo? Ele é um conjunto unitário. Agora, reparem que por A ser subconjunto de B, quando a diferença entre A e B é calculada, todos os elementos de A são eliminados, não restando nenhum elemento no conjunto. Neste caso, A – B é um conjunto vazio.  

Conseguiram entender a ideia? Vejam que em nenhum dos exemplos vistos até agora, os conjuntos A – B e B – A foram iguais. Isso nos mostra que a propriedade comutativa não é válida para a diferença entre dois conjuntos, ou seja:

 

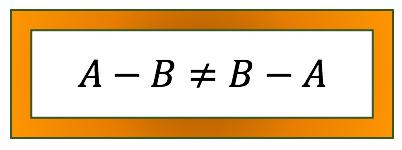
Bom, depois de tudo o que acabamos de discutir, não há dúvidas de que esse texto está chegando ao fim! Agradeço imensamente a atenção de vocês, e espero que o que vimos aqui, somado ao que vocês verão agora no vídeo que está em anexo, seja muito proveitoso para os seus estudos!

O Complementar de um Conjunto também pode ser encontrado através da operação de diferença entre os conjuntos. Se vocês quiserem saber mais sobre o assunto, é só acessar este texto.

A teoria dos conjuntos é base para toda a matemática do ensino médio. Portanto, vocês já podem se considerar mais próximos daquela nota ótima desejada no ENEM e nos vestibulares!

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abraço! Bons estudos em matemática!