CONSEQUÊNCIAS DA DEFINIÇÃO DE UM LOGARITMO

Olá pessoal! Como vão?

Algumas configurações de logaritmos podem ser facilmente resolvidas quando conhecemos bem a definição e as condições de existência dessa operação. São as consequências da definição dos logaritmos, por isso nós vamos estudá-las uma a uma nesse texto. Conhecer cada uma delas é de extrema importância para os seus estudos, pois o assunto costuma ser muito cobrado, direta ou indiretamente, nas provas do ENEM e dos vestibulares!

Por acaso vocês conhecem a plataforma do Professor Ferretto? Ela dispõe de um módulo exclusivo que trata do estudo dos logaritmos, além de outros 22 módulos que abordam todo o conteúdo de matemática do ensino médio. E se o objetivo de vocês é gabaritar a matemática do ENEM ou do vestibular, fica mais fácil por lá, pois é possível montar um plano de estudos com foco na prova que irão realizar! Acessem o site e confiram todas as formas de aprofundar o conhecimento!

Bom, se nós vamos abordar as consequências de uma definição, então precisamos conhecer bem a definição de que estamos tratando, não é? Observem o quadro abaixo com atenção:

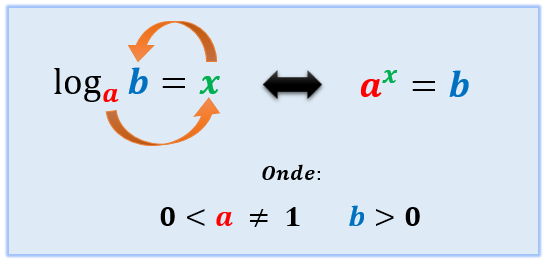
Da maneira como o logaritmo é definido neste quadro, nós podemos dizer que o termo a é a sua base, o termo b o seu logaritmando e x o logaritmo ou o resultado da operação. Ainda, temos que lembrar de algumas restrições que os valores de a e b possuem. A base a deve ser sempre um valor maior que zero e diferente de 1, enquanto que o logaritmando b deve ser necessariamente um valor maior que zero. Assim, através do processo de logaritmação, nós podemos dizer que a base a elevada ao expoente x resulta no valor de b, o logaritmando.

Antes de continuarmos, aqui vai uma dica bem importante: se todas as informações que acabamos de revisar não ficaram tão claras para vocês, não deixem de dar uma olhadinha no texto Introdução aos Logaritmos. Lá vocês encontram tudo sobre a nomenclatura dos termos dos logaritmos e sobre a sua definição. Agora se o problema for a resolução dos logaritmos em si, não deixem de conferir o texto Aplicando a Logaritmação. Lá são resolvidos detalhadamente inúmeros exercícios para vocês não terem dúvidas quando precisarem aplicar esse conhecimento!

Certo pessoal!? Agora que já relembramos a definição dos logaritmos, vamos as suas consequências. Vou mostrar cada uma delas a vocês, sempre deixando claro de onde foi que todos os raciocínios foram retirados.

O logaritmo da unidade, em uma certa base a, é sempre igual a zero.

Assim, podemos concluir que quando o logaritmando de um certo logaritmo for igual a 1, seja qual for o valor da base a, que esteja, é claro, de acordo com as restrições (0 < a ≠ 1), o resultado será zero. Querem saber porquê? Vamos supor que o resultado do logaritmo de 1 na base a seja um certo valor x.

Nosso dever agora é resolver esse logaritmo. Utilizaremos as setinhas para levar o logaritmo a sua forma exponencial. Uma vez que isso é alcançado, buscaremos uma maneira de obter uma igualdade de potências de mesma base, do jeitinho que aprendemos no texto Equação Exponencial. Tudo isso é feito para que possamos trabalhar apenas com os expoentes, igualando-os, vejam só:

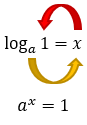
Chegamos a nossa equação exponencial, não é? Mas como fazer com que o número 1 seja reescrito como uma potência de base a? O fato é que nesse caso, devemos lembrar que qualquer número elevado ao expoente zero é igual a 1. Bom, se qualquer número elevado a zero resulta em 1, a elevado a zero também resulta em 1, e, portanto, temos que:

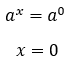
Tranquilo não é? Vamos a mais uma consequência da definição dos logaritmos!

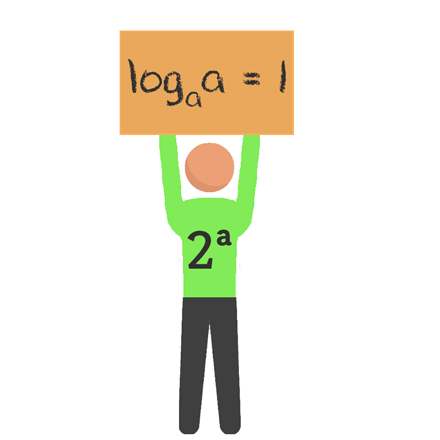
Se em um logaritmo, o valor do logaritmando for exatamente igual ao valor da base, então o seu resultado será sempre um.

Assim, sempre que observarmos um logaritmo cuja base e logaritmando possuírem o mesmo valor, e reforço novamente, estando esse valor de acordo com as restrições (0 < a ≠ 1), não é necessário se preocupar com a resolução, o resultado é com toda a certeza a unidade, 1. Para entendermos como isso é possível, iremos supor, novamente, que o resultado do logaritmo de a na base a será x e iremos resolver a operação:

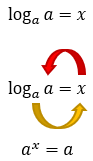
Chegamos a uma igualdade de potências de mesma base, restando-nos igualar os expoentes e trabalhar apenas com eles. Aí vocês poderiam perguntar: mas onde está o expoente de uma das bases a?  É só lembrar do seguinte: quando um expoente não aparece, significa que ele vale 1, e desta forma nós concluímos que:

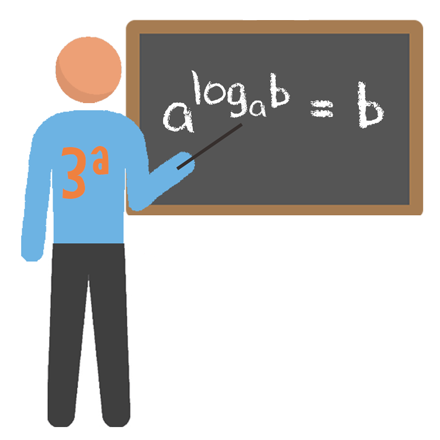
Se o expoente de uma potência for um logaritmo, e o valor da base desse logaritmo for igual ao da base da potência, então o resultado será o próprio logaritmando.

Ficou difícil de imaginar que dedução poderia levar a essa conclusão, não é? A verdade é que tudo partiu de uma igualdade de logaritmos, que quando submetidos a logaritmação, resultam no que acabamos de aprender. Vou mostrar para vocês como isso é possível:

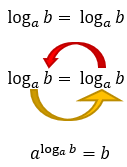
Quanto a dedução, podemos dizer que é bem simples, certo? Mas como memorizar todos esses detalhes na hora de aplicar essa consequência? Simples também! Se liguem nessa dica que vou mostrar agora utilizando alguns exemplos.

Reparem que em ambos os logaritmos apresentados acima, o valor da base da potência é igual ao valor da base do logaritmo. Neste caso, nós podemos cortar ou cancelar, o valor da base da potência com o logaritmo e sua base, e nos restará apenas o logaritmando, vejam só:

É claro pessoal que matematicamente, esse cancelamento não faz sentido algum. Isso é apenas uma técnica que utilizamos para lembrar que em casos como esse, o resultado é o próprio logaritmando do logaritmo.

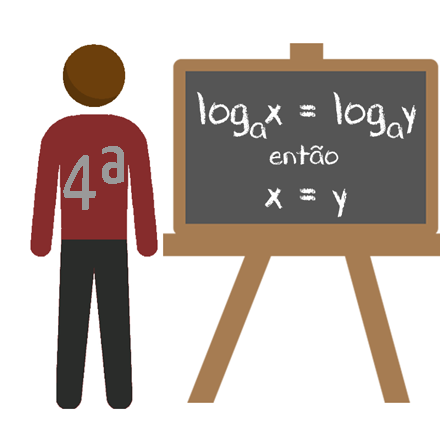
Quando houver uma igualdade de logaritmos de mesma base, é possível trabalhar apenas com os logaritmandos, igualando-os.

Para que essa quarta consequência fique um pouco mais clara, vamos resolver um exercício:

Calcule o valor de x tal que log₂ (x – 3) = log₂ 3.

Pessoal, reparem que esse é justamente um caso onde temos uma igualdade de logaritmos de mesma base. De acordo com a consequência que acabamos de aprender, quando isso acontecer podemos trabalhar apenas com os logaritmandos, igualando-os, vejam só:

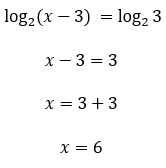
Bom, chegou o momento em que vamos aplicar tudo que vimos até agora através de alguns exercícios. Vem comigo aqui!

Calcule o valor de:

O primeiro detalhe que precisamos reparar aqui, é que existe um logaritmo no expoente de uma potência. Sendo assim, em que consequência da definição dos logaritmos essa questão poderia se encaixar? Na terceira, é claro! Assim, para resolver o caso, devemos trabalhar para fazer com que o valor da base da potência seja igual ao da base do logaritmo. Ora, 16 = 2⁴. Então podemos substituir esse valor no cálculo:

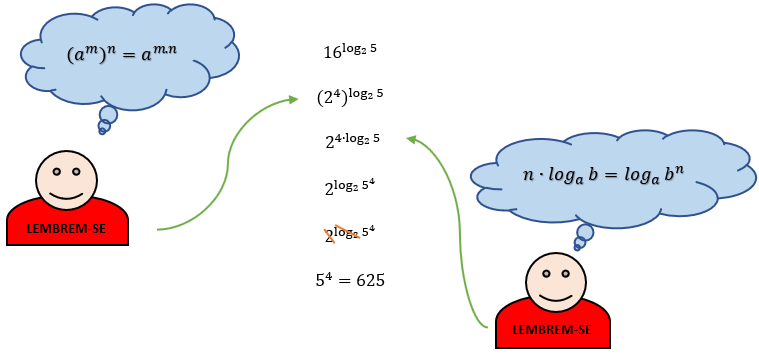
Vejam como o cálculo que acabamos de fazer ficou extremamente simples quando fizemos uso de uma das consequências da definição, além de algumas propriedades da potenciação e dos logaritmos. Se nós tivermos conhecimento sobre esses três fatores, nenhuma questão poderá nos deter! Vamos confirmar isso resolvendo mais um exercício.

Novamente encontramos uma potência, e no seu expoente temos a presença de um logaritmo. É claro que a única consequência da definição que se encaixa ao caso é a 3ª que estudamos, mas reparem que dessa vez encontramos também uma soma no expoente da potência. Para resolver esse impasse, primeiramente faremos o uso de mais uma propriedade da potenciação, olhem só:

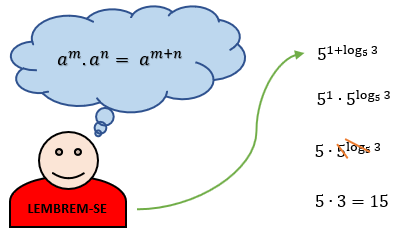
Agora, para finalizarmos o texto com chave de ouro, vamos avaliar algumas sentenças e verificar se elas são verdadeiras ou falsas.

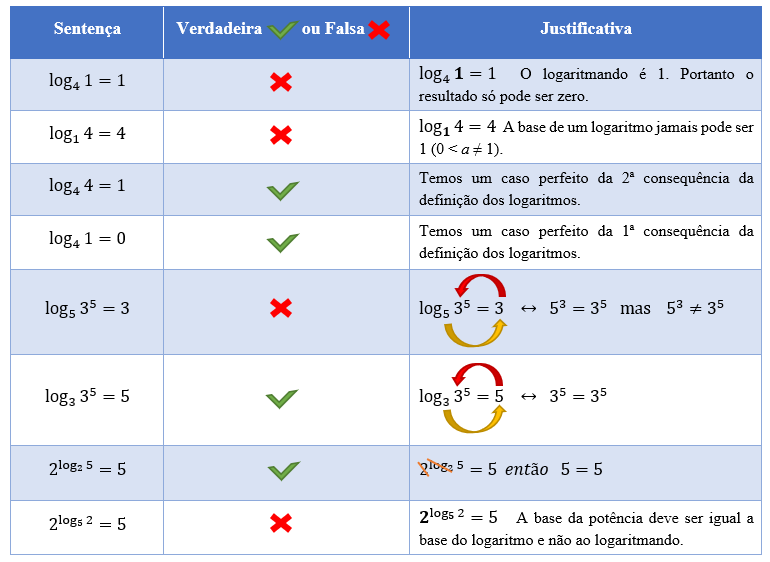
E assim concluímos mais um texto! Espero que ele tenha sido muito proveitoso para os seus estudos, e que agora seja mais fácil de memorizar todas essas regrinhas, que podem nos poupar um grande trabalho. Em anexo, é claro, temos o vídeo desse conteúdo. Deem uma olhadinha nele, lá vocês acompanharão outros exemplos e uma abordagem que complementa esse texto.

Um abração! Tenham ótimos estudos em matemática, e até logo!