O losango é um quadrilátero cujos 4 lados possuem a mesma medida. Por isso, pode-se dizer que todo o quadrado é um losango, e não fosse a diferença no valor dos ângulos internos de ambas as figuras, também poderia se afirmar o contrário.

 

Olá, pessoal! Tudo bem com vocês?

Por um acaso vocês já repararam nas figuras geométricas da bandeira do Brasil? Pois então, aquela de cor amarela é o quadrilátero notável que vamos estudar hoje, o losango! Neste texto, falaremos sobre todas as propriedades do losango e sobre como é possível calcular a sua área. Esses conceitos são extremamente simples, mas de uma importância enorme para quem é estudante do ensino médio e está buscando uma vaga no ensino superior.

Entendido, pessoal? Então, para quem não conhece, esse é o losango!

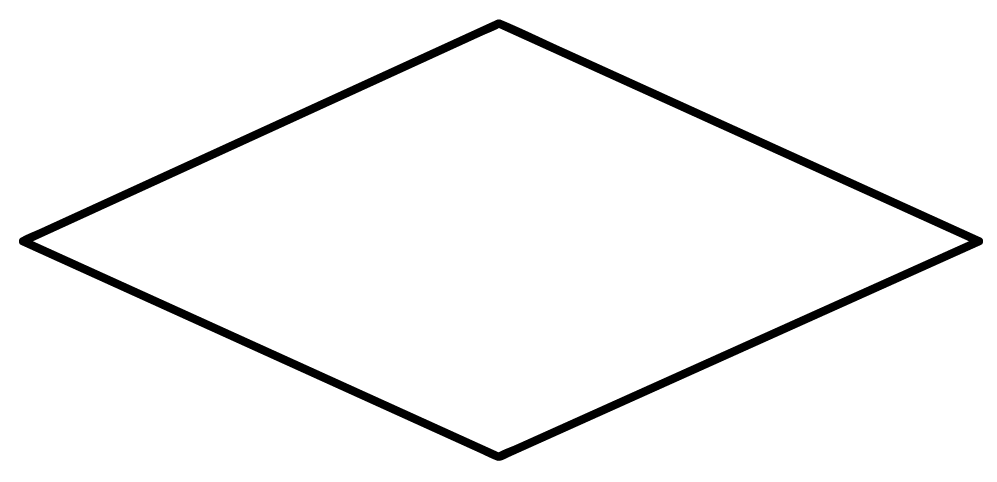
Vamos iniciar nossos estudos conhecendo todas as propriedades desse quadrilátero. Venham comigo!

 

1. PROPRIEDADES DO LOSANGO

Nem todo paralelogramo é um losango, mas todo losango é considerado um paralelogramo. Por isso, algumas propriedades do losango também são comuns aos paralelogramos em geral, enquanto outras pertencem exclusivamente a ele. É chegada a hora de estudarmos cada uma dessas propriedades com detalhes. Vamos lá!

 

1.1 Em todo losango os dois lados opostos são sempre paralelos e congruentes

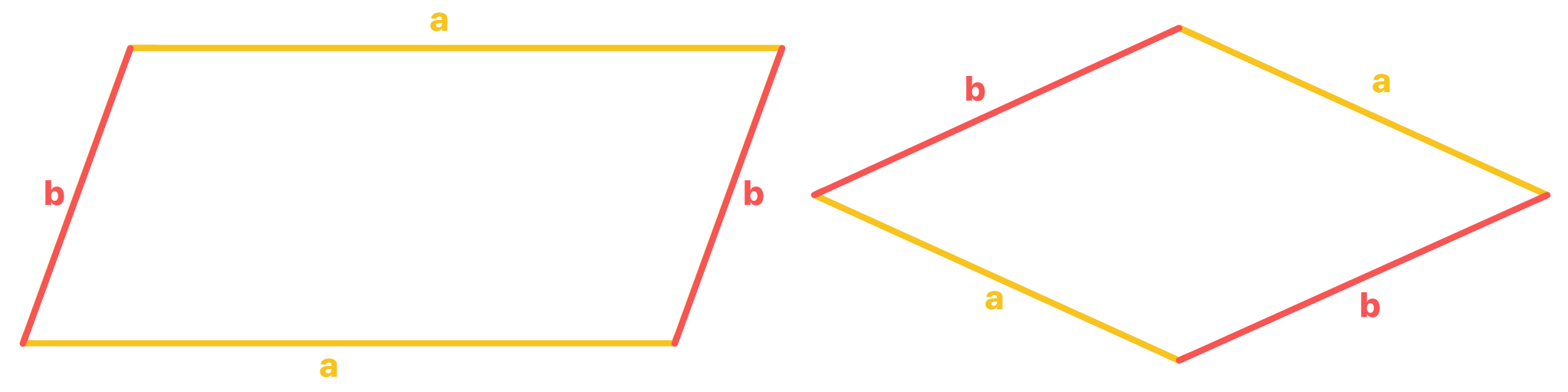
Essa propriedade nos mostra que os dois lados opostos de um losango são sempre paralelos e de mesma medida. Aliás, aí vai uma dica: todo quadrilátero que possui os dois lados opostos paralelos é um paralelogramo! É daí que vem o nome!

 

1.2 Todo losango possui os seus quatro lados congruentes

Os quatro lados de um losango possuem o mesmo comprimento l. E aí vocês poderiam se perguntar: mas isso não acontece com o quadrado também? Claro que sim! Por isso é possível dizer que todo quadrado é um losango, e que todas as propriedades do losango também são válidas para o quadrado!

 

1.3 Em todo losango as diagonais interceptam-se nos seus pontos médios

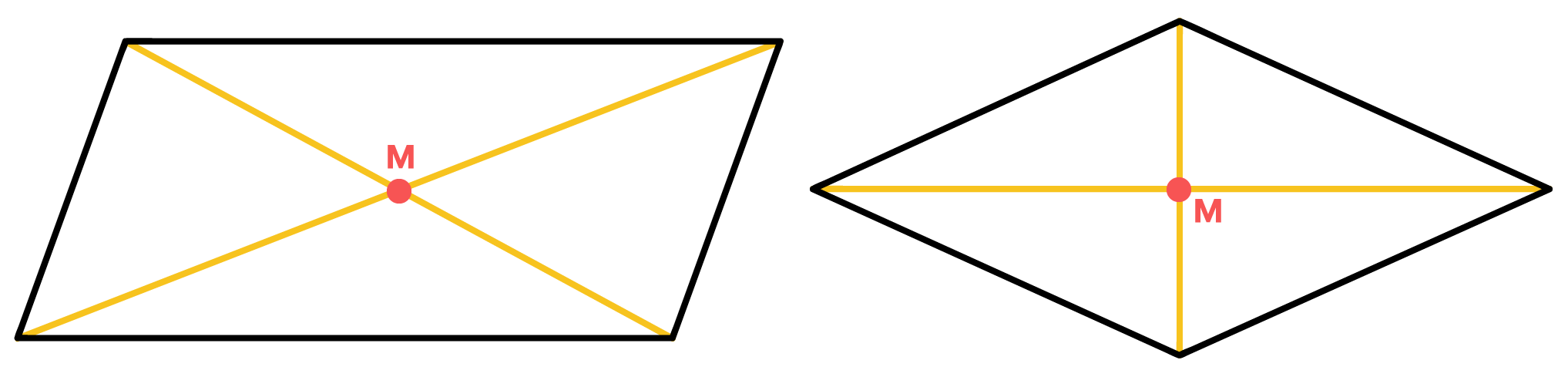
As diagonais dos losangos, e de qualquer outro paralelogramo, cortam-se exatamente em seus respectivos pontos médios. Isso significa que de cada vértice do losango, até o ponto M, tem-se a metade da medida da diagonal total correspondente.

Incrível, não é mesmo? Mas as diagonais do losango, exclusivamente, possuem outras características interessantes. Todo losango possui duas diagonais, mas sempre haverá uma diagonal de comprimento maior do que a outra. É por isso que nomeamos elas como D e d. A diagonal maior é representada pela letra D maiúscula, enquanto que a diagonal de comprimento menor é representada pela letra d minúscula.

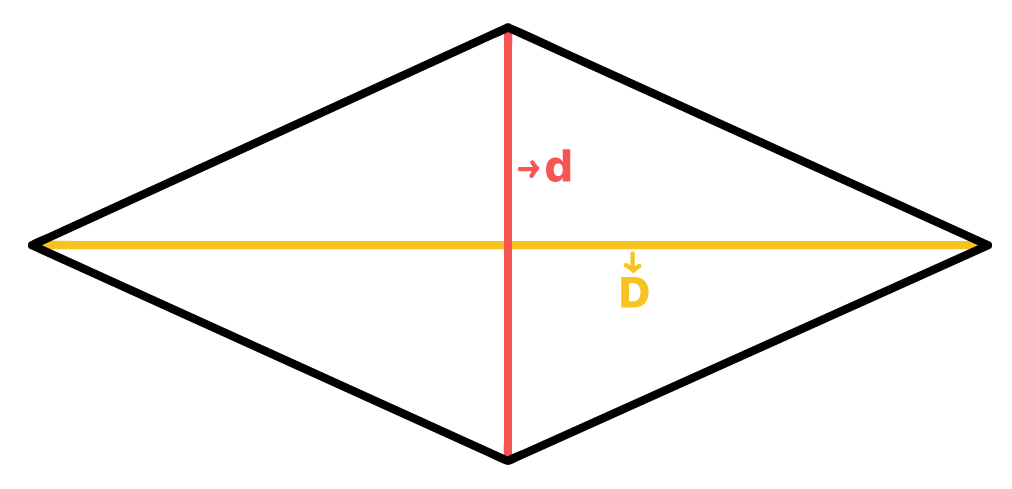
Pessoal, isso é uma questão de visualização mesmo! Tudo vai depender de como o losango está posicionado, mas não vale a pena se preocupar com isso. A forma como vocês nomearem as diagonais não vai interferir em nenhuma das fórmulas que serão apresentadas aqui!

 

1.4 As diagonais do losango são perpendiculares entre si

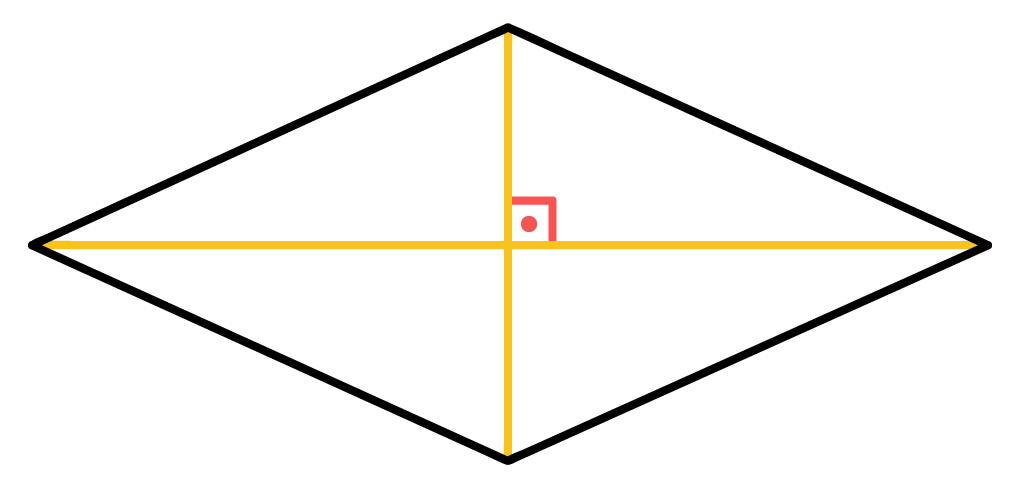
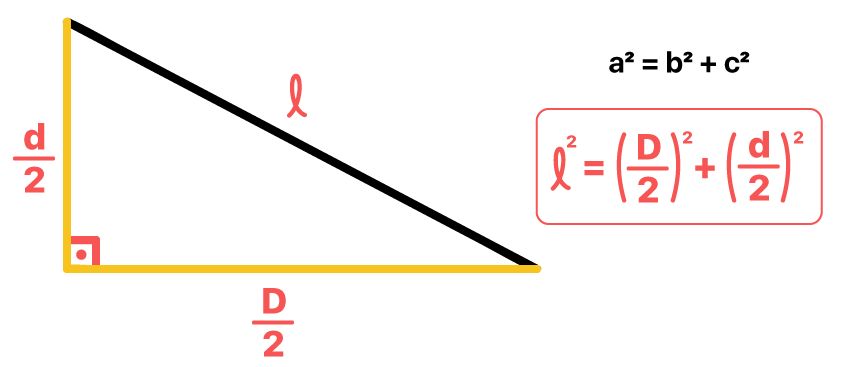
Através desta propriedade, pode-se compreender que diagonais do losango formam um ângulo de 90º entre si, dividindo esta figura em quatro triângulos retângulos iguais. Bom, é fato que todo triângulo retângulo está estritamente relacionado com o Teorema de Pitágoras. Por isso, esse teorema poderá ser utilizado para associarmos a medida l do lado do losango, com a metade da medida de cada uma de suas diagonais.

“O quadrado da medida da hipotenusa é igual a soma dos quadrados das medidas dos catetos”

 

1.5 Em todo losango os dois ângulos opostos são sempre congruentes

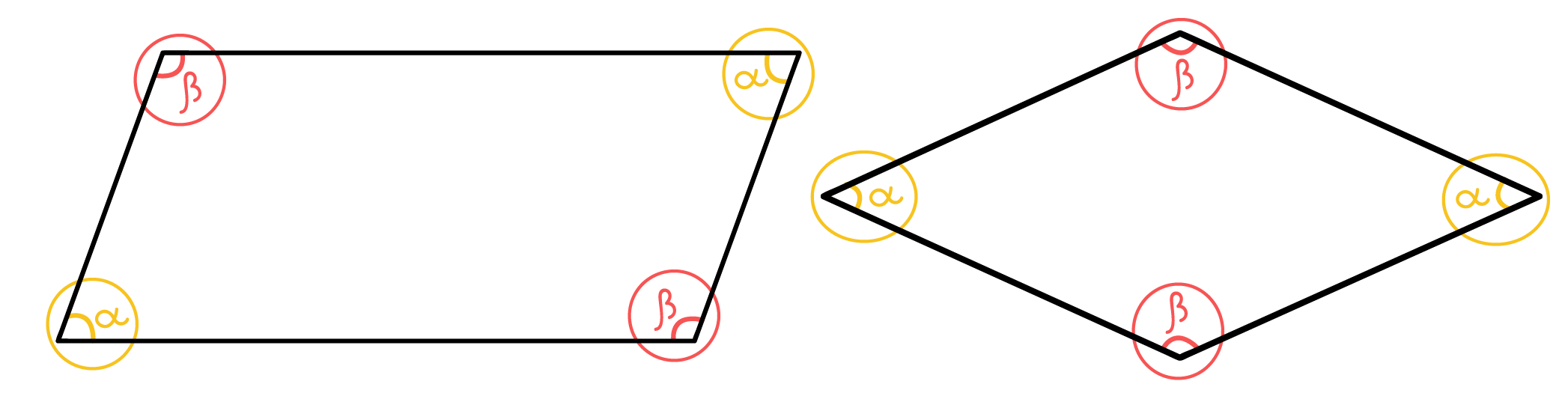
Como pode ser visto na imagem, os dois ângulos opostos de qualquer losango são sempre iguais, ou têm a mesma medida. Bom, essa propriedade vale para qualquer paralelogramo. Mas além disso, reparem que os ângulos que nomeamos como α são menores que 90º, ou seja, são agudos, enquanto que os ângulos que chamamos de β são maiores que 90º, isto é, são obtusos. Se o valor de β fosse reduzido, e o de α fosse aumentado, a ponto de ambos serem iguais a 90º, teríamos a nossa frente um quadrado!

Legal, não é? Na próxima propriedade, vamos conhecer mais uma característica interessante que envolve os ângulos e as diagonais do losango.  É só vir comigo!

 

1.6 As diagonais do losango são bissetrizes dos seus vértices

Uma bissetriz é uma reta que divide um ângulo em duas partes iguais. Assim, sendo as diagonais bissetrizes dos vértices do losango, na medida em que cada uma delas parte de um dos vértices deste quadrilátero rumo ao seu vértice oposto, acaba por dividir os dois ângulos α e β pela metade. Desta forma, surgem quatro ângulos iguais, de medida α/2 e β/2.

 

1.7 Em todo losango dois ângulos consecutivos são sempre suplementares

Dois ângulos são suplementares, se a soma de seus valores resultar em 180º. Assim, podemos dizer que no losango e em qualquer paralelogramo:

α + β = 180˚

 

2. FÓRMULA DA ÁREA DE UM LOSANGO

A forma como a área do losango é definida tem tudo a ver com outro quadrilátero muito conhecido, aquele que está contornando o losango na figura acima. Pode ser que vocês ainda não tenham reparado na relação que o retângulo e o losango têm, por isso, vamos ver se a figura abaixo consegue deixar isso mais claro.

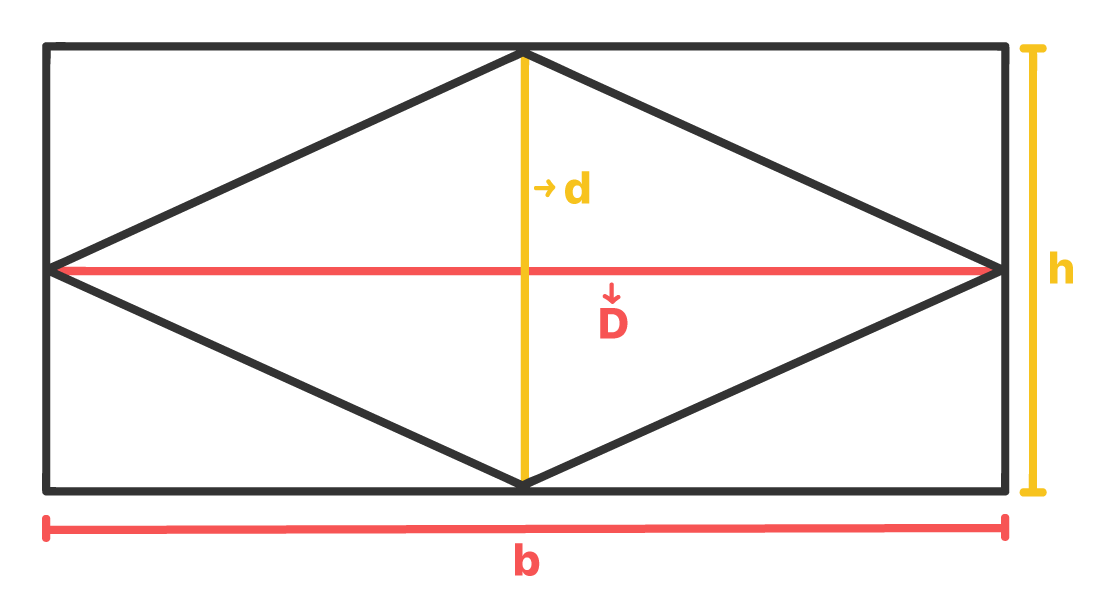
Ao desenharmos as diagonais do losango, duas coisas ficam evidentes: a primeira delas é que a medida da diagonal maior do losango, D, é exatamente igual a medida da base b do retângulo. Como não podia ser diferente, a medida da diagonal menor do losango, d, é exatamente igual a medida da altura h do retângulo.

Além disso, é fato que as diagonais do losango o dividem em 4 triângulos retângulos iguais, como já vimos anteriormente neste texto. Mas o mais impressionante aqui, é que se prestarmos atenção na área do retângulo que não pertence ao losango, veremos que ela é composta por outros 4 triângulos retângulos iguaizinhos àqueles que compõem o losango, olhem só:

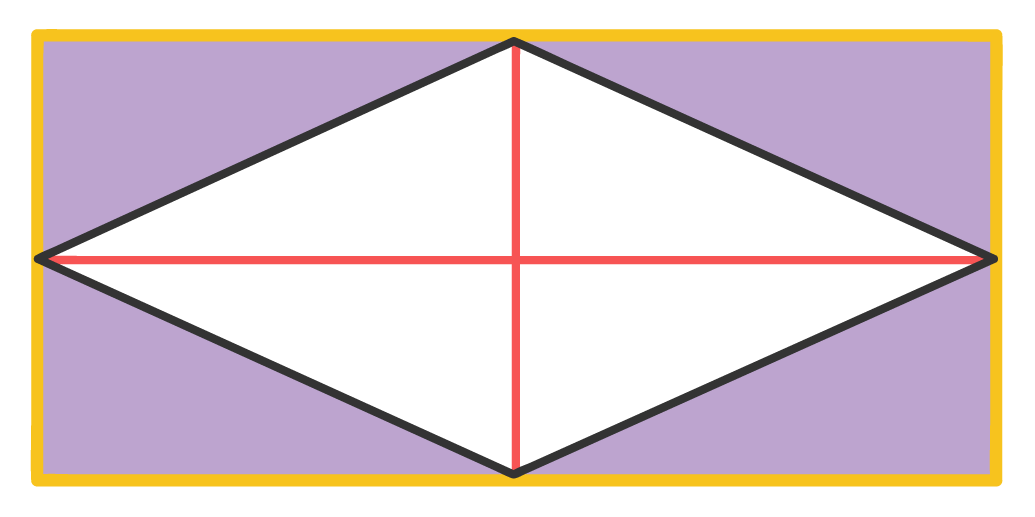
Portanto, podemos concluir que com um único retângulo é possível formar dois losangos! Por consequência, é claro que o losango possui exatamente a metade da área do retângulo. E como a área do retângulo é dada pelo produto da medida de sua base pela medida de sua altura, podemos chegar à fórmula da área do losango da seguinte forma:

Pode-se dizer, então, que a área do losango é dada pela metade do produto de suas diagonais.

Certo, pessoal?! Chegou o momento de aplicarmos todos os conhecimentos adquiridos hoje. Vamos resolver um exercício juntos. Vem comigo aqui!

 

3. EXERCÍCIO RESOLVIDO SOBRE O LOSANGO

Num losango, a soma dos ângulos obtusos é o dobro da soma dos agudos. Se a diagonal menor do losango mede 12 cm, determine o seu perímetro e a sua área.

 

Pessoal, a primeira coisa a se fazer quando estamos resolvendo qualquer exercício de geometria é desenhar as informações que o enunciado traz. Começaremos focando nos ângulos do losango.

O enunciado nos diz que a soma dos ângulos obtusos é o dobro da soma dos agudos. Bom, segundo a 5ª propriedade que estudamos neste texto, os dois ângulos opostos de um losango são sempre congruentes. Além disso, é fato que o ângulo α possui uma abertura um pouco menor que 90º, enquanto β possui uma abertura um pouco maior que 90º. Portanto, α é um ângulo agudo, e β é um ângulo obtuso. Sendo assim, podemos transformar a informação dada na seguinte equação:

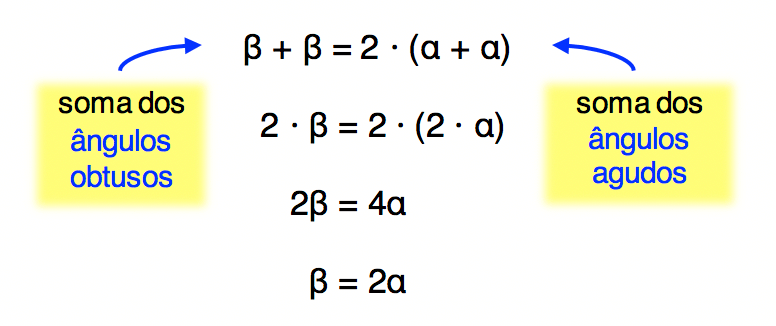
Até aí, tudo certo? Apesar de termos montado uma equação muito interessante, reparem, ainda estamos em função dos dois ângulos α e β. Desta forma, para resolvermos o problema, precisamos procurar mais alguma informação sobre os ângulos do losango. E não é que a 7ª propriedade que estudamos relata que dois ângulos consecutivos do losango são sempre suplementares? Pois bem, então é fato que:

α + β = 180 °

Substituindo na fórmula dos ângulos suplementares o valor de β obtido na primeira equação que montamos, temos que:

α + 2∙α = 180°

3∙α = 180°

α = 60°

Assim:

β = 2∙α

   β = 120°

Aí fica a pergunta: como é que vamos descobrir a área e o perímetro do losango apenas com o valor de seus ângulos? Felizmente, sabendo que a medida da diagonal menor do losango é 12 cm, podemos resolver o problema de duas formas diferentes. Acompanhem cada uma delas comigo!

 

1ª Forma de resolver o problema

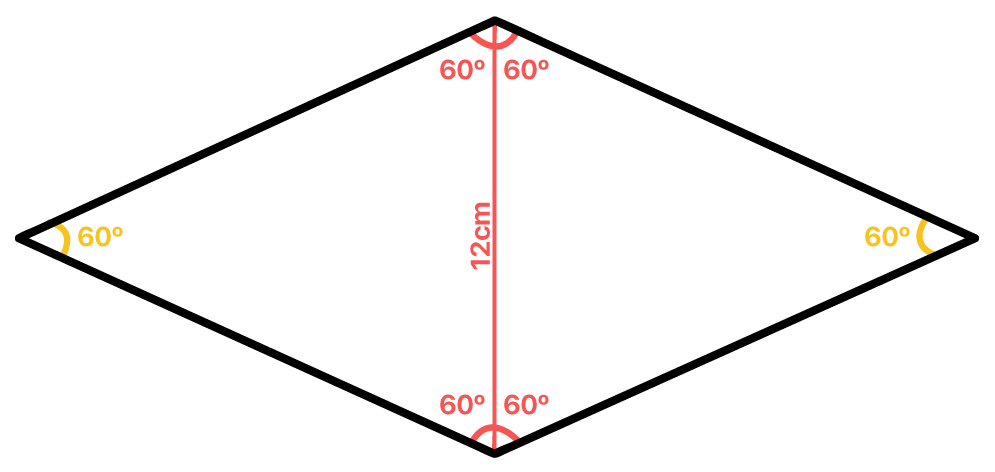
Já que conhecemos a medida da diagonal menor do losango, por que não a ilustrar em nosso desenho para ver o que acontece? Incrivelmente, ao fazermos isso, nos deparamos com o conhecimento abordado na 6ª propriedade que estudamos: a diagonal do losango divide o ângulo β pela metade!

Curiosa essa figura formada, não é mesmo? Como neste losango o ângulo β é equivalente ao dobro do ângulo α, quando traçamos a sua diagonal menor, acabamos dividindo o mesmo em dois triângulos cujos ângulos internos são todos iguais. Acontece que só existe um tipo de triângulo em que isso é possível: no triângulo equilátero!

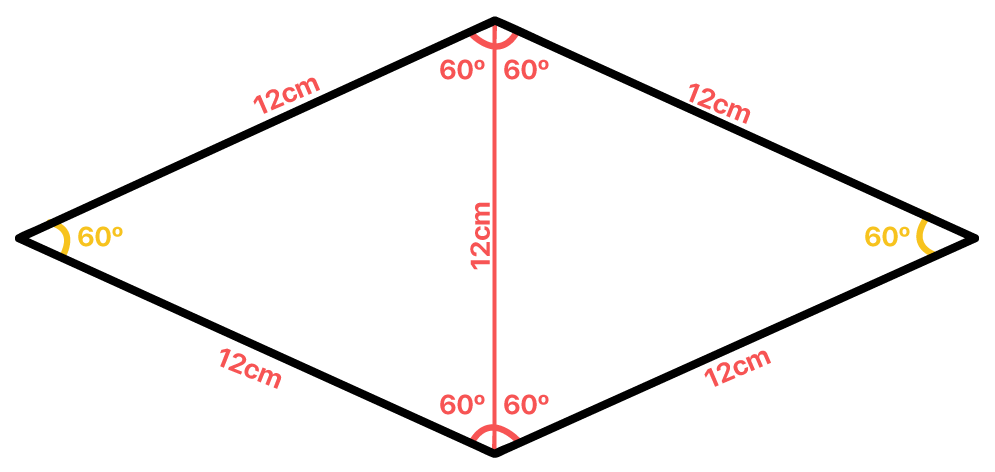
O triângulo equilátero, como o próprio nome sugere, é aquele cujos 3 lados e os 3 ângulos internos possuem a mesma medida. Isso nos permite concluir que o lado l do losango mede 12 cm também.

Sabendo que o perímetro de qualquer figura geométrica é dado pela soma do comprimento de todos os seus lados, já temos condições de calcular o perímetro deste losango:

P = l + l + l + l

P = 4∙l

P = 4∙12

P = 48 cm

Agora, só nos resta calcular a área do losango. Nesta primeira forma de resolver a questão, vamos utilizar o mesmo conceito que nos levou a descobrir a medida do seu lado l: o triângulo equilátero. É fato que o losango desse exercício é composto por 2 triângulos equiláteros. Então, se nós descobrirmos a área desse triângulo e a multiplicarmos por 2, certamente teremos o valor da área procurada. Acompanhe comigo:

 

2ª Forma de resolver o problema

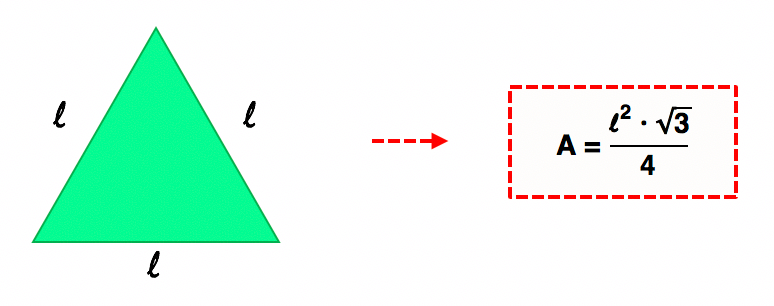
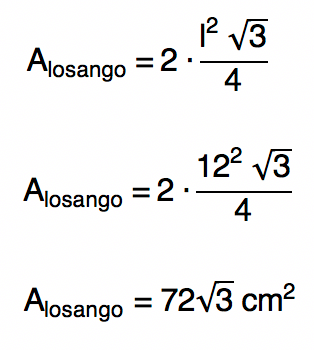
Vamos supor agora a seguinte situação: vocês identificaram que a diagonal menor do losango o divide em dois triângulos equiláteros, e assim, descobriram que o lado do losango também mede 12 cm. Tendo isso por base, calcularam o perímetro do losango, mas quando chegou a hora de calcular a área não perceberam que ela podia ser obtida através da área do triângulo equilátero.

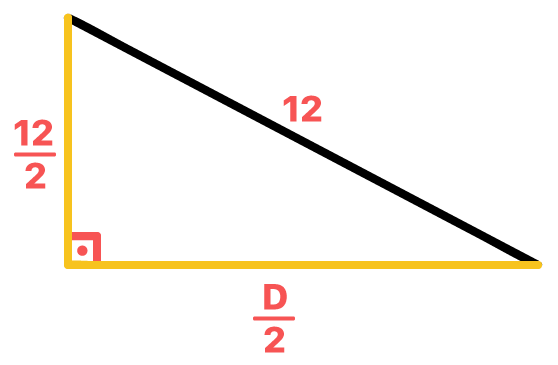
Sem problemas, pessoal! Também podemos resolver esse problema considerando um detalhe muito interessante que aprendemos na 4ª propriedade deste texto. Como as diagonais do losango são perpendiculares entre si, podemos formar 4 triângulos retângulos dentro do mesmo. Utilizando o Teorema de Pitágoras em qualquer um deles, é possível encontrar a medida da diagonal maior do losango, D. Lembram da fórmula que vimos lá em cima? Pois chegou a hora de utilizarmos ela!

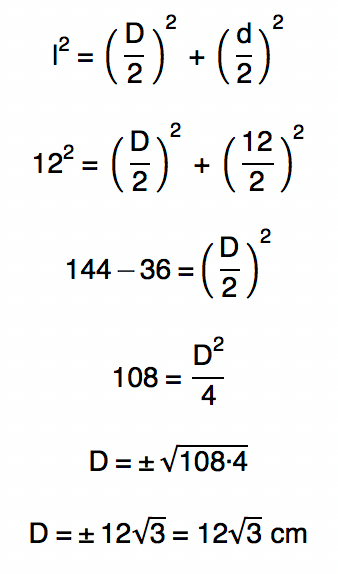
Agora, é possível encontrar a área do losango utilizando a sua própria fórmula da área, olhem só:

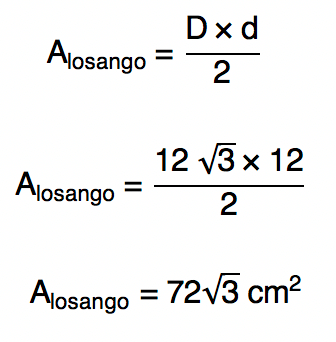
E aí, o que acharam do texto de hoje? Se você gostou deste conteúdo, clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Espero que tudo o que estudamos os ajude a desvendar a geometria plana com mais facilidade a partir de hoje! E claro, em anexo, fica o vídeo que trata do assunto. Deem uma olhada nele, pois lá são resolvidos mais alguns exercícios que unem os conceitos de losango à trigonometria e à semelhança entre triângulos.

Um forte abraço, pessoal! Até breve!