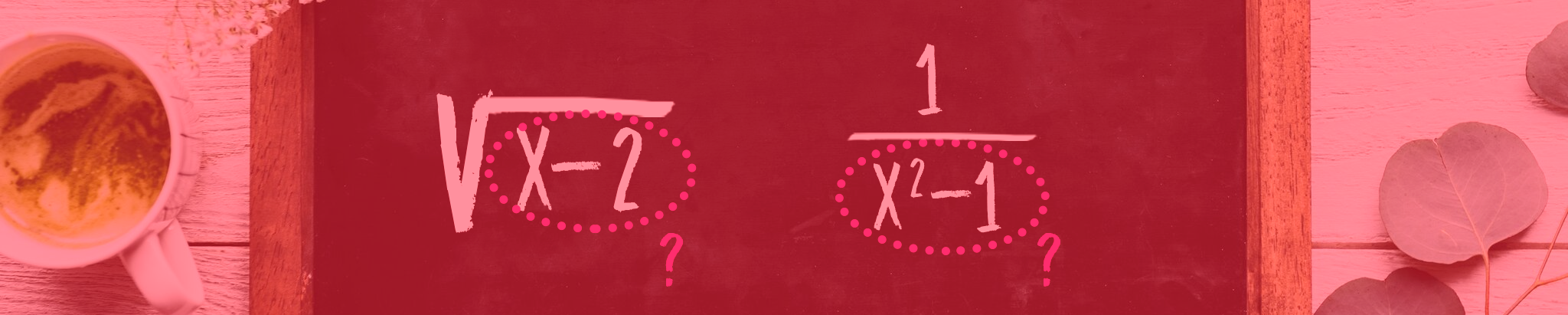Não é extremamente necessário saber se uma função é afim, quadrática, exponencial, modular ou logarítmica, para que seja possível esboçar o seu gráfico. Com 5 passos simples, dá para construir o gráfico de qualquer função matemática!

Olá, pessoal! Tudo tranquilo?

Toda função matemática possui uma representação gráfica que a identifica, e que a torna única em meio a diversas outras funções. Lembram da famosa foto 3×4 que nos identifica nos documentos? Pois então, o gráfico é a foto de uma função! É claro que conhecer as características principais de alguns tipos de funções pode ajudar a definir o seu formato gráfico. Contudo, quem acompanhar este texto vai aprender como construir gráficos de uma maneira geral, utilizando alguns passos bem simples. Aí, se aparecer aquela função esquisita nas provas do ENEM e dos vestibulares, não haverá problema algum, porque vocês terão o conhecimento básico para esboçar o seu gráfico!

Beleza, pessoal? Então, vamos conhecer os tão esperados passos que vão nos ajudar a construir diversos gráficos. Vem comigo!

1. DESENHAR O PLANO CARTESIANO

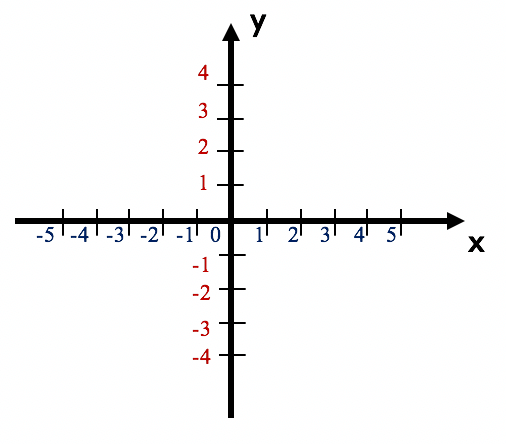
Nós vimos no texto Noções Básicas de Plano Cartesiano, que o plano cartesiano é um sistema utilizado para especificar pontos e determinar localizações ou posições dentro de determinado “espaço” ou superfície. Já que a construção de gráficos é mesmo fundamentada na obtenção de pontos relacionados com o domínio e a imagem de uma função, nada mais justo do que utilizarmos o plano como base para realizar essa tarefa, concordam?

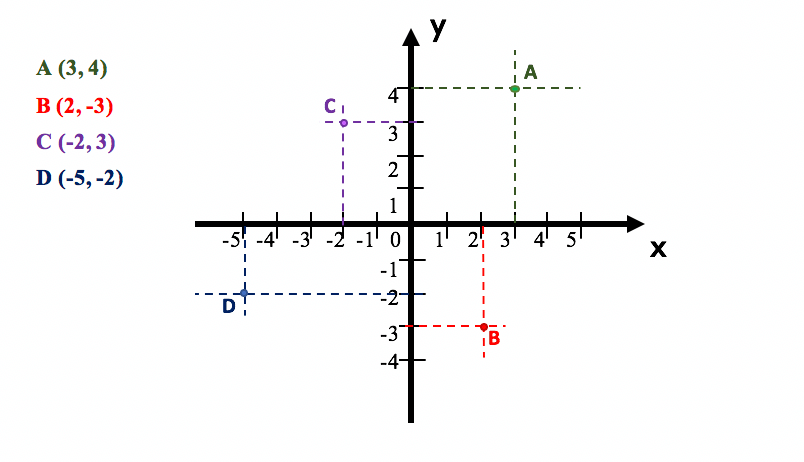
O plano cartesiano é formado por duas retas numéricas perpendiculares entre si. Uma delas é conhecida como eixo x, ou eixo das abscissas, e a outra como eixo y, ou eixo das ordenadas. Cada ponto que é traçado no plano cartesiano, costuma ser chamado de par ordenado, na forma P(x,y). Isso significa que a ordem em que os elementos são dispostos importa. Portanto, o primeiro elemento do par ordenado P deverá representar sempre o valor que será marcado em relação ao eixo x, enquanto que o segundo elemento do par ordenado P representará sempre o valor que será marcado em relação ao eixo y. Observem a imagem abaixo.

2. DETERMINAR O DOMÍNIO DA FUNÇÃO

Como foi dito no item anterior, o esboço de gráficos é fundamentado na obtenção de pares ordenados relacionados com o domínio e a imagem de uma função. Então, o que estamos esperando? Vamos descobrir como encontrar esse tal de domínio!

O domínio de uma função sempre será formado pelos valores numéricos que podem substituir o lugar da sua variável, geralmente chamada de x, e ainda assim, fazer com que a função exista! Se vocês lerem os meus pensamentos acima, verão que em alguns casos o domínio das funções é apresentado com clareza, seja na forma de conjunto com elementos finitos, ou na forma de conjunto numérico como um todo.

Quando o domínio da função não é evidente

Mas é claro que nem tudo na vida são flores! Por isso, quem observou meus pensamentos com atenção, viu que eu também lembrei de algumas funções diferentes, cujo domínio não foi apresentado. Quando isso acontece, vocês é que devem determinar o domínio da função, o que requer alguns cuidados importantes:

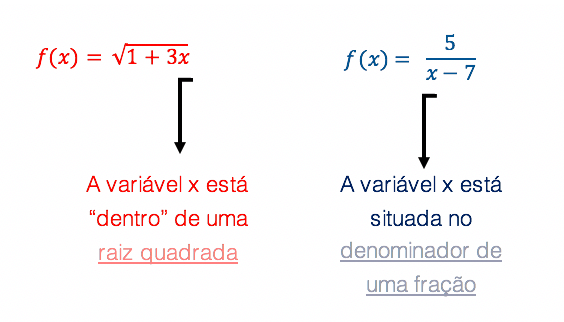
Pessoal, quando realizamos operações tais como a adição, a subtração ou a multiplicação, não há restrição alguma quanto aos valores numéricos que utilizamos. Contudo, quando se trata das operações de divisão, ou mesmo de radiciação com índice par, as coisas mudam um pouquinho. Não existe, por exemplo, dentro do conjunto dos números reais, raiz quadrada de número negativo, e muito menos divisão por zero! Por isso, ao nos depararmos com funções como as que vemos acima, devemos excluir do domínio qualquer valor numérico que possa substituir o lugar de x e gerar um radicando negativo, ou um denominador igual a zero.

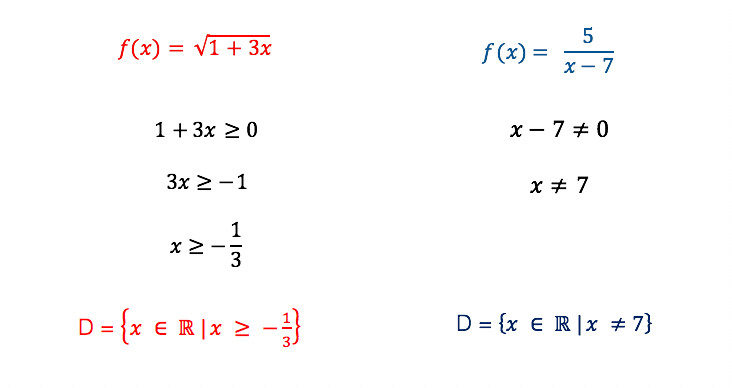
Ou seja, é tudo uma questão de análise! Mas se a função cujo gráfico devemos construir não possuir restrições, esse passo fica mais simples. Qualquer valor real poderá substituir o lugar de x e fazer parte do seu domínio!

3. ENCONTRAR ALGUNS PARES ORDENADOS

Vejam que ao abordar o domínio de uma função, nós falamos um monte sobre a variável x. E não é que o primeiro elemento do par ordenado P(x,y) é justamente o x? Ou seja, conhecer o domínio da função cujo gráfico deve ser realizado, nos dá a noção de quais valores poderão ser marcados em relação ao eixo x no plano cartesiano.

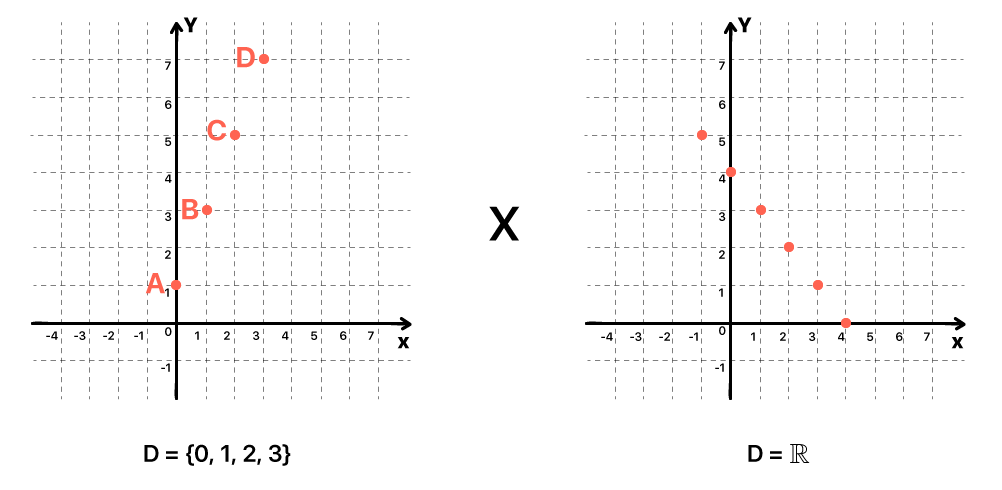
Assim, com o auxílio de uma tabela, é possível substituir a variável x da lei de formação da função por valores numéricos pertencentes ao seu domínio. Dessa forma, serão gerados valores reais correspondentes em f(x) ou em y, que pertencem a imagem da função, completando o tão esperado par ordenado P(x, y). Esse processo é exemplificado na imagem abaixo.

A função que aparece no exemplo, ƒ(x) = 2x + 1, tem como característica um domínio limitado, ou seja, composto apenas por alguns valores definidos. Por isso, ao montarmos as tabelas, utilizamos apenas os valores dados para obtermos pares ordenados. Mas o fato é que é muito mais comum encontrarmos casos como os dos outros exemplos que temos citado, em que o domínio das funções é dado por conjuntos numéricos inteiros, ou com a exclusão de poucos elementos. Aí, devido a imensa gama de valores que temos à disposição, podemos ficar à vontade para escolher alguns daqueles que mais nos convém.

Dentre todos os números reais, eu sugeri que escolhêssemos –1, 0, 1, 2, 3 e 4. Mas o fato é que vocês poderiam adotar quaisquer outros valores. Ainda assim, teríamos a formação do mesmo gráfico, acreditem!

3.1 Dicas ninja do Ferretto

E aí, repararam que na última imagem do tópico anterior surgiu uma segunda tabela, menor, e com apenas duas colunas? Pois então, de tanto construir gráficos, uma hora ou outra os cálculos serão feitos de cabeça. Por isso a tabela fica com apenas duas colunas,   com os valores de x a esquerda e os valores de y a direita. Isso diminui a chance de nos confundirmos ao traçar o par ordenado,  simplifica e agiliza o processo.

Além disso, existe outro detalhe do qual vocês devem lembrar sempre. Qualquer ponto que se localiza exatamente sobre o eixo das abscissas tem a configuração (x, 0). Da mesma forma, qualquer ponto que se localiza exatamente sobre o eixo das ordenadas,  tem a configuração (0, y). Portanto, substituir x e y por zero, pode ser uma ótima jogada para não desenhar o gráfico em regiões muito distantes dos eixos do plano cartesiano!

4. TRAÇAR OS PARES ORDENADOS NO PLANO CARTESIANO

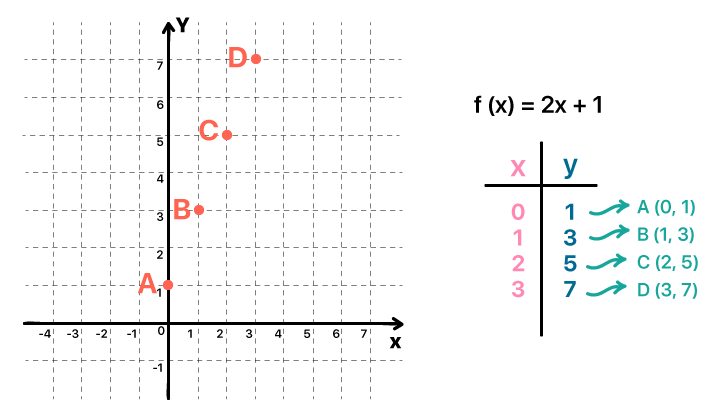
Depois que os pares ordenados foram encontrados, o jeito é marca-los no plano cartesiano, como vemos na imagem acima. Para facilitar a visualização dos pontos, vocês podem dar nomes a eles, utilizando as letras do alfabeto, por exemplo. Só não dá para esquecer que o primeiro elemento dos pares ordenados deverá representar o valor que será marcado em relação ao eixo x, enquanto que o segundo elemento dos pares ordenados representará sempre o valor que será marcado em relação ao eixo y. Depois que o assunto estiver dominado, talvez não seja mais necessário dar nome aos pontos no plano. Fiquem atentos a imagem seguinte.

5. LIGAR OS PONTOS, CONCLUINDO O ESBOÇO DO GRÁFICO

É, o título do último passo que devemos tomar é mesmo bastante sugestivo. Para concluir o esboço de qualquer gráfico, devemos ligar os pontos que encontramos. Mas é aí que mora um detalhe bem intrigante: nem sempre isso acontece! Por isso a importância do passo número 2, em que obtemos o domínio da função.

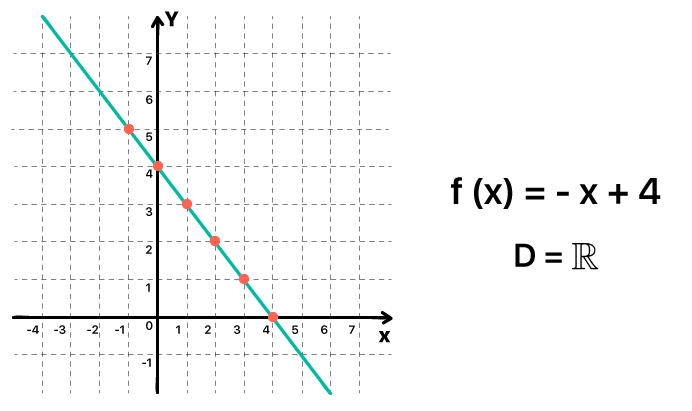
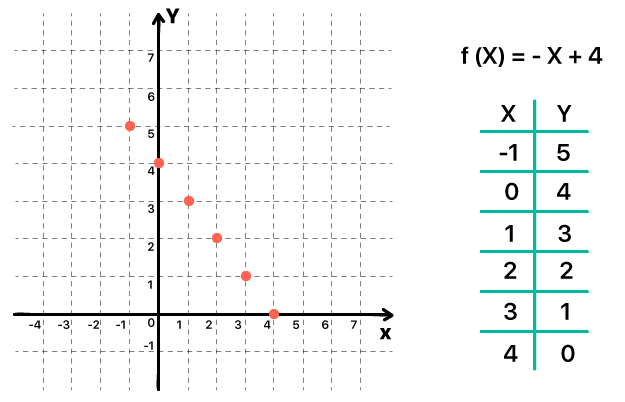
A função ƒ(x) = – x + 4 possui como domínio todo o conjunto dos números reais. Isso significa que podemos ligar todos os pontos e seguir traçando o gráfico antes e depois deles, afinal, qualquer valor que substituir x permite que a função exista. Contudo, quando o domínio da função é limitado, como no caso da função ƒ(x) = 2x+ 1, somente para os valores 0, 1, 2, e 3 a função existe. Aí não podemos de forma alguma ligar os pontos encontrados, e o gráfico fica assim mesmo, como mostra a imagem abaixo.

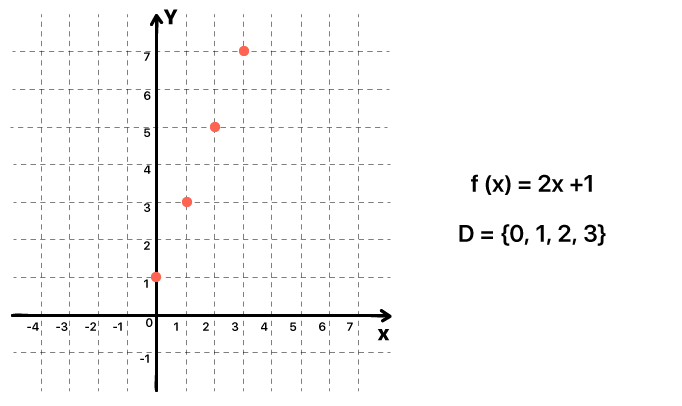
Isso não é uma loucura? Pois é, pessoal, as vezes a matemática nos prega mesmo algumas peças. Mas não existe razão para se assustar: no vídeo que deixo em anexo, vocês acompanham com mais detalhes a construção desses gráficos, e de quebra, resolvem comigo mais alguns exemplos bem interessantes!

E se você gostou do conteúdo, aproveite também para conhecer a Plataforma do Professor Ferretto! Clique aqui para saber como ela funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Por fim, espero que este texto tenha contribuído para aprimorar o conhecimento de vocês no assunto. Toda a semana eu estou de volta com muito mais matemática de qualidade!

Um abração a todos e ótimos estudos!