INEQUAÇÕES MODULARES – PARTE 1
26/12/2018
As inequações modulares, são todas as relações de desigualdade em que a incógnita se encontra dentro de módulos. Estas inequações podem ser resolvidas facilmente, desde que se conheça o conceito de módulo de um número real.
Olá, pessoal, tudo bem por aí?
Vocês sabiam que o módulo de qualquer número real jamais pode ser negativo ou menor do que zero? Pois bem, no texto de hoje, eu vou mostrar para vocês que esse conceito é a base para a resolução de qualquer inequação modular, da mais simples, a mais complexa! É claro que as consequências da definição de módulo que nós veremos aqui, também podem facilitar, e muito, o desenvolvimento deste tipo de inequação. Então, já deu pra perceber que este texto está cheinho de conteúdo interessante, não é mesmo?
É, só existe uma coisa melhor do que saber tudo sobre as inequações modulares: conhecer toda a matemática do ensino médio! Depois que a geometria, a probabilidade, a análise combinatória, as funções, a trigonometria e tantos outros assuntos estão dominados, não há como ter erro nas provas do ENEM e dos vestibulares. E o mais legal de tudo, é que é bem fácil ter todo esse material em mãos: basta assinar a plataforma do Professor Ferretto! Lá tem exercícios resolvidos, planos de estudos, ranking por curso, e até aulas de física! Quem quiser conhecer todas as vantagens que o curso disponibiliza, não vai se arrepender: é rapidinho, basta acessar o site!
| x | ≥ 0
E agora, chegou a hora de começarmos nosso estudo! A expressão acima, define algebricamente aquilo que temos enfatizado desde o início do texto: o módulo de qualquer número real resultará sempre em um valor positivo ou igual a zero!
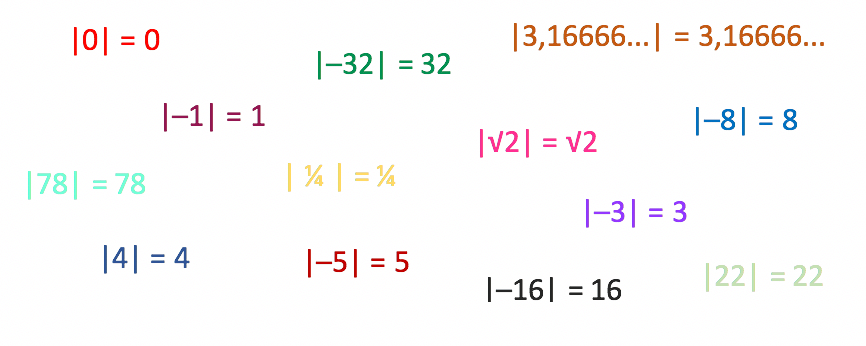
Tendo isso em vista, qual seria a solução para as inequações que apresento abaixo? Vem comigo!
1. | x | ≥ – 3
Essa expressão não está requisitando nada mais nada menos do que possíveis valores de x cujo módulo seja maior ou igual a –3. Ora, se o módulo de qualquer número real resulta sempre em valores maiores ou iguais a zero, parece lógico que qualquer valor real que substitua x gere como resultado valores maiores que –3, afinal, o zero em si já é um número maior que –3.
S = ℝ
Pronto! Nesse caso, qualquer valor real pode satisfazer a desigualdade. Viram como foi só uma questão de lógica? Então fiquem atentos ao próximo exemplo!
2. | x | ≤ – 3
Mas que coisa estranha! A expressão acima pede que nós busquemos valores de x cujo módulo seja menor ou igual a –3. Só que nós acabamos de aprender, que não existem valores de x nos quais o módulo seja menor que zero ou negativo. Assim, já que nenhum valor real consegue satisfazer a inequação, o seu conjunto solução será dado através do famoso conjunto vazio.
S = ø
3. | x | ≥ 0
Essa inequação representa justamente a definição de módulo, lembram? Por isso, podemos afirmar, com toda a certeza, que qualquer número real satisfaz a desigualdade: o módulo de qualquer número real é sempre um valor positivo ou igual a zero!
S = ℝ
4. | x | > 0
Opa! Esse exemplo se torna extremamente intrigante quando conseguimos enxergar com clareza a diferença dele em relação ao anterior: aqui, estão sendo questionados os valores de x cujo módulo resulte em valores maiores do que zero, e não maiores ou iguais a zero. Bom, se levarmos em conta que o único valor cujo módulo resulta em zero é o próprio zero, nós conseguiremos definir que qualquer outro valor real que não seja ele, produzirá um módulo positivo, como está sendo pedido. Essa conclusão dá origem a um conjunto solução interessante: o conjunto dos números reais quando o zero é excluído.
S = ℝ*
Feito, pessoal? Antes de partirmos para o próximo exemplo, aí vai uma sugestão: caso vocês queiram conhecer melhor a representação dos conjuntos numéricos que excluem o número zero, ou mesmo os números positivos e negativos, é só dar uma olhada no texto Números Naturais e Inteiros! Lá vocês encontram informações sobre alguns subconjuntos notáveis bem inspiradores!
5. | x | < 0
Existe algum valor de x cujo módulo seja negativo ou menor do que zero? Não, né? Por isso, nosso amigo conjunto vazio deverá entrar em cena novamente.
S = ø
6. | x | ≤ 0
Este é mais um daqueles exemplos que podem gerar uma grande confusão! Olhando rapidamente, poderíamos ter considerado o sinal de menor com um indício de que a solução não daria certo. Mas é justamente aí que mora o perigo! O sinal menor ou igual (≤), nos oferece duas opções: ou encontramos valores de x cujo módulo seja menor que zero, ou encontramos valores de x cujo módulo seja igual a zero. Quanto a primeira ideia, é claro que não tem jeito, mas sabemos que que a segunda possibilidade nos reserva uma saída: ao substituirmos x por zero, podemos gerar um resultado igual a zero! Isso significa que o nosso conjunto solução será um conjunto unitário, ou seja, um conjunto que possui apenas um único elemento, o zero:
S = {0}
E aí, pessoal, tudo claro até aqui? Vejam quantas soluções nós conseguimos definir só por questão de lógica, e claro, tendo em mente o conceito de módulo de um número real. Isso já nos ajuda bastante, mas o fato é que nem sempre ocorrerão casos em que solução possa ser dada simplesmente por todo o conjunto dos números reais, ou pelos conjuntos vazio e unitário. Por essa razão, apresento a vocês uma segunda alternativa. Vem comigo aqui!

Levando em consideração as consequências da definição de módulo descritas acima, fica fácil de resolver outras tantas inequações modulares que surgirem no nosso caminho! Reparem que o primeiro passo, consiste em observar se o valor numérico que se encontra a direita da desigualdade é mesmo maior que zero ou positivo. Se isso for confirmado, basta ver em qual dos casos a inequação se encaixa, e montar a reta real correspondente. Para ficar mais claro, vamos resolver os exemplos abaixo aplicando esta técnica, acompanhem comigo!
7. | x | < 3
Neste exercício, nós precisaremos encontrar os possíveis valores de x cujo módulo seja menor do que 3. 3 é um valor maior que zero, o que significa que podemos utilizar o método que acabamos de aprender, contudo, em qual dos 4 casos esta inequação se encaixa? Como está sendo utilizado o sinal de desigualdade menor (<) em relação ao módulo, podemos utilizar o primeiro caso para resolver a situação:
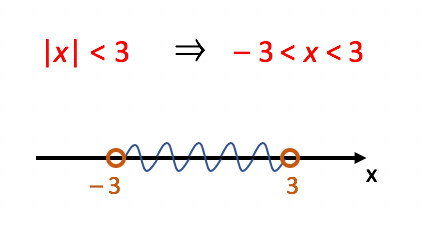
Agora é só fazer alguns testes! Se nós substituirmos x por algum valor que esteja na faixa entre –3 e 3, a desigualdade deve ser satisfeita. Do contrário, ou seja, se substituirmos x por um valor fora da faixa, a desigualdade não poderá ser satisfeita de nenhuma forma, ou nossa solução não estaria correta. Felizmente, as notícias serão boas, olhem só:

Viram como deu certo? Isso nos permite escrever o conjunto solução da questão:
S = {x ∈ ℝ| –3 < x < 3}
8. | x | ≥ 4
Da mesma forma que no exemplo anterior, o valor numérico que se encontra no lado direito da desigualdade é maior que zero, ou positivo! Hora de voltarmos a imagem mais acima para comprovarmos que essa inequação se encaixa no 4º e último caso.
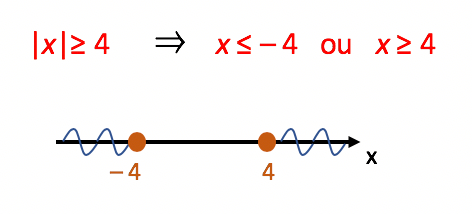
Vou aproveitar esse exemplo para deixar uma tarefa de casa para vocês: tendo por base o exemplo anterior, façam o teste e comprovem a solução deste caso. Ao substituir x por um valor maior ou igual a 4, ou por um valor menor ou igual a –4, o módulo gerado deve necessariamente ser um valor maior ou igual a 4. Do contrário, ou seja, se um valor entre –4 e 4 for escolhido, o módulo resultante não deverá satisfazer a desigualdade!
S = {x ∈ ℝ| –4 ≤ x ≤ 4}
Um último detalhe importante a ser observado, é que ao contrário do exemplo anterior, os valores 4 e –4 entraram no conjunto solução. Isso aconteceu, porque temos um sinal de maior ou igual na inequação. Aí fica o alerta: se o sinal de igual aparecer, as bolinhas na reta real são fechadas, e os valores base da solução entram no conjunto!
Feito, pessoal? Então acho que já podemos encerrar esse texto! Espero que todos os conceitos vistos aqui tenham sido proveitosos para os seus estudos, e que vocês consigam se basear neles para enfrentar os desafios que por ventura surgirem! É claro que em anexo, fica aquele vídeo que complementa tudo o que foi abordado, então não deixem de dar uma olhadinha nele antes de ir!
No mais, vale lembrar que tem muito mais conteúdo sobre a função modular aqui no blog! Quem está pensando em garantir aquela nota no ENEM e nos vestibulares, não pode perder nenhum texto!
Um abração! Nos vemos logo logo!