
Quais sĂŁo as propriedades da matĂ©ria? Veja exemplos e exercĂcios resolvidos As propriedades da matĂ©ria sĂŁo as caracterĂsticas, os comportamentos...

Os sistemas de equaçÔes de duas incógnitas podem ser resolvidos através dos métodos da adição e da substituição. Saiba tudo sobre esses dois métodos aqui!
Os sistemas de equaçÔes são conjuntos de duas ou mais equaçÔes que possuem as mesmas incógnitas, e, portanto, admitem a mesma solução. Os métodos mais utilizados na resolução de sistemas de equaçÔes de duas incógnitas são o método da adição e o método da substituição.
Â
OlĂĄ, pessoal! Como vĂŁo?
Estamos aqui hoje para estudar um assunto de extrema importĂąncia para a matemĂĄtica. As equaçÔes do primeiro grau sĂŁo aplicadas em muitas situaçÔes do cotidiano, quando Ă© necessĂĄrio encontrar um valor desconhecido. Contudo, em alguns problemas dois valores numĂ©ricos sĂŁo desconhecidos, sendo obrigatĂłria a resolução de duas equaçÔes do primeiro grau simultaneamente. Assim, formam-se os sistemas de duas equaçÔes, que vamos aprender a resolver neste texto!Â
Beleza, pessoal? Logo mais, nós vamos aprender a resolver os sistemas de equaçÔes de duas incógnitas de duas formas diferentes. Acompanhem comigo o passo a passo de cada método e também os exemplos que vamos solucionar.

A essĂȘncia do mĂ©todo da adição consiste em somar as duas equaçÔes do sistema de forma que a soma de uma das incĂłgnitas seja igual a zero. Para que isso seja possĂvel, essa incĂłgnita deve ter, nas duas equaçÔes, o mesmo valor em mĂłdulo, mas sinais opostos. Vamos resolver um sistema de duas equaçÔes seguindo o passo-a-passo do mĂ©todo.
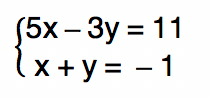
Reparem no sistema acima, que nem a incĂłgnita x e nem a incĂłgnita y possuem valores iguais em mĂłdulo, mas com sinais opostos. Portanto, se somĂĄssemos as equaçÔes desse jeito, nĂŁo seria possĂvel eliminar qualquer uma das incĂłgnitas:
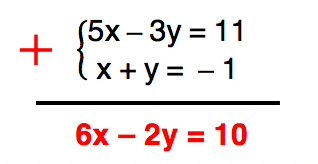
Assim, para resolvermos este impasse, podemos, por exemplo, multiplicar a segunda equação do sistema por â 5, de forma a eliminar a incĂłgnita x. Outra solução poderia ser multiplicar a segunda equação do sistema por 3, de modo a eliminar a incĂłgnita y. Vamos utilizar aqui essa segunda solução.
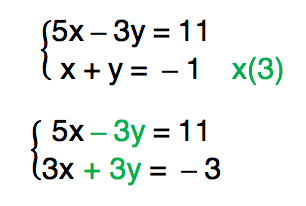
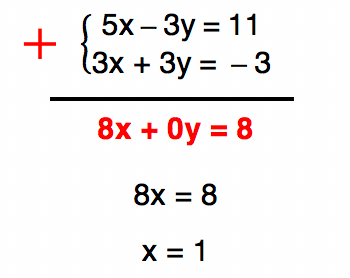
Como no caso do exemplo a incĂłgnita y foi eliminada, foi possĂvel encontrar o valor numĂ©rico de x. No prĂłximo passo, concluĂmos a resolução encontrando o valor de y.
Aqui, vamos substituir o valor de x na segunda equação inicial, de forma a obter o valor de y.
x + y = â 1
1 + y = â 1
y = â 2
Assim, o conjunto solução do sistema Ă© dado por S = {(1, â 2)}.
Pessoal, Ă© muito importante evidenciarmos aqui, que chegamos a esse resultado efetuando uma sĂ©rie de escolhas. Mas na verdade, vocĂȘs poderiam seguir qualquer outro caminho dentro desses mesmos passos. O importante Ă© que o resultado obtido seja o mesmo, entendido?
Bom, para provar que existem vĂĄrios meios de se chegar a mesma solução, vamos resolver agora o mesmo sistema de equaçÔes atravĂ©s do mĂ©todo da substituição. Estudem todos os passos com calma e avaliem qual dos mĂ©todos funciona melhor para vocĂȘs. Vamos lĂĄ!

Como o prĂłprio nome sugere, a essĂȘncia do mĂ©todo da substituição consiste em isolar uma das incĂłgnitas em uma das equaçÔes e substituir essa mesma incĂłgnita pelo valor algĂ©brico encontrado na outra equação. Vamos ver como isso acontece direitinho acompanhando com atenção os passos seguintes.
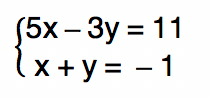
Â
Nesse passo, pessoal, vocĂȘs poderiam isolar qualquer incĂłgnita em qualquer uma das equaçÔes. Contudo, pode ser mais interessante escolher a equação e a incĂłgnita mais fĂĄcil de isolar dentro do conjunto. Quando as incĂłgnitas estĂŁo acompanhadas do nĂșmero 1, fica mais simples de realizarmos todo o cĂĄlculo, jĂĄ que o valor algĂ©brico obtido nĂŁo serĂĄ formado por uma fração.
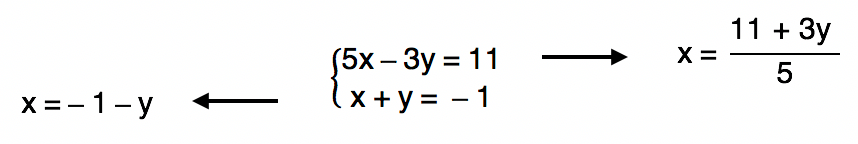
Observem no sistema que poderĂamos isolar a incĂłgnita x de duas maneiras diferentes. Se fizermos isso na primeira equação, teremos como resultado um valor algĂ©brico fracionĂĄrio. Com toda a certeza poderĂamos seguir para o prĂłximo passo e utilizar esse valor. Contudo, ao isolar a incĂłgnita x na segunda equação, encontramos um valor algĂ©brico muito mais simples que o outro. Por isso, vamos seguir a resolução do sistema tomando como base o valor algĂ©brico de x igual a ââ 1 â yâ.
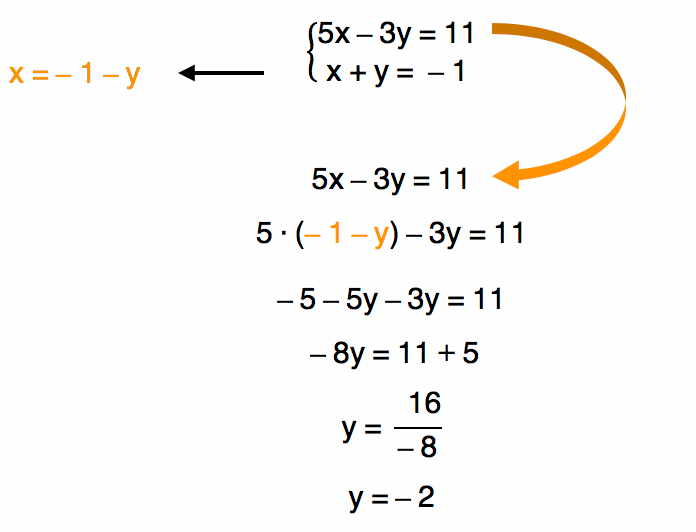
Como isolamos a incĂłgnita x da segunda equação no passo anterior, substituĂmos o seu valor algĂ©brico na primeira equação. Isso nos possibilitou encontrar o valor numĂ©rico de y. Como base nesse valor, podemos seguir para o prĂłximo passo.
Â
Aqui, pessoal, vocĂȘs podem substituir o valor numĂ©rico de y na primeira equação â5x â 3y = 11â, ou mesmo na segunda equação âx + y = â 1â. Para ficar ainda mais simples, vamos substituir o valor de y na equação que montamos ao isolar a incĂłgnita x.
x = â 1 â y
x = â 1 â (â 2)
x = 1
Assim, o conjunto solução do sistema Ă© dado por S = {(1, â 2)}.
Legal, nĂŁo Ă©, pessoal? Utilizamos dois mĂ©todos diferentes, mas, chegamos ao mesmo resultado final. Por isso, vocĂȘs podem optar pelo mĂ©todo que acharem mais conveniente. Vamos resolver agora mais alguns sistemas de equaçÔes de duas incĂłgnitas para que vocĂȘs tenham ainda mais afinidade com o tema. Vem comigo!

Antes de encerrarmos o texto, vamos resolver dois sistemas de equaçÔes utilizando o mĂ©todo da substituição e o mĂ©todo da adição. Pode ser que as decisĂ”es tomadas aqui nĂŁo sejam o caminho utilizado por vocĂȘs, contudo, lembrem sempre que o mais importante Ă© chegar no mesmo conjunto solução no final.
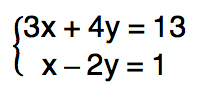
Método da substituição
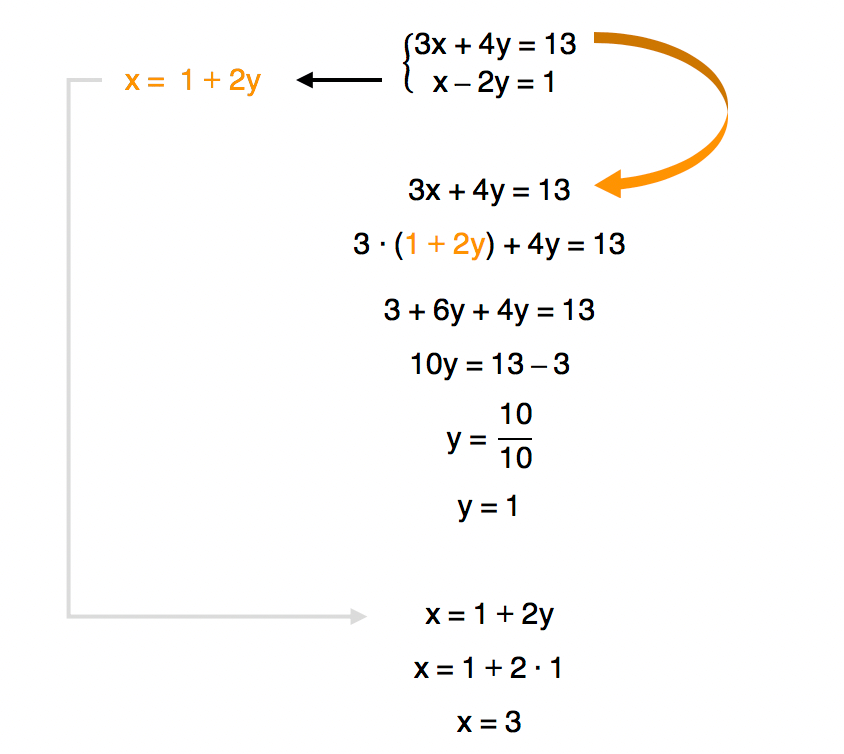
Assim, o conjunto solução do sistema é dado por S = {(3, 1)}.
Método da adição
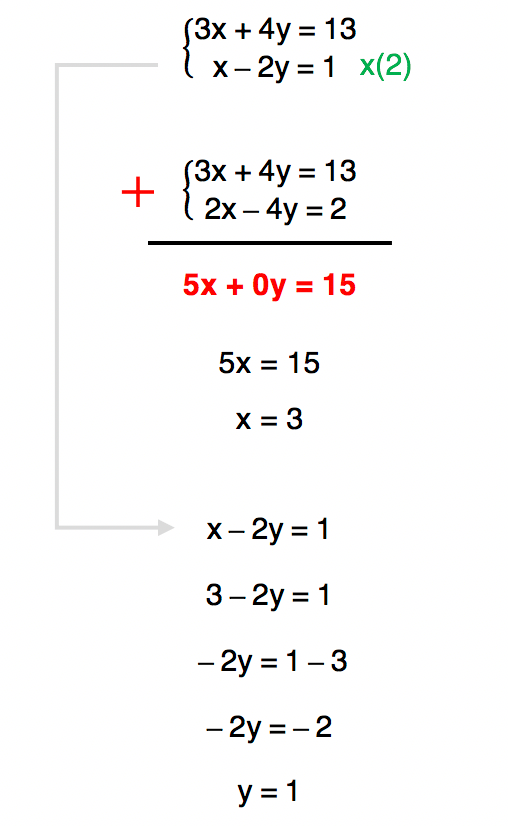
Da mesma forma, o conjunto solução do sistema é dado por S = {(3, 1)}.
Â
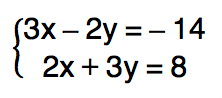
Â
Método da substituição
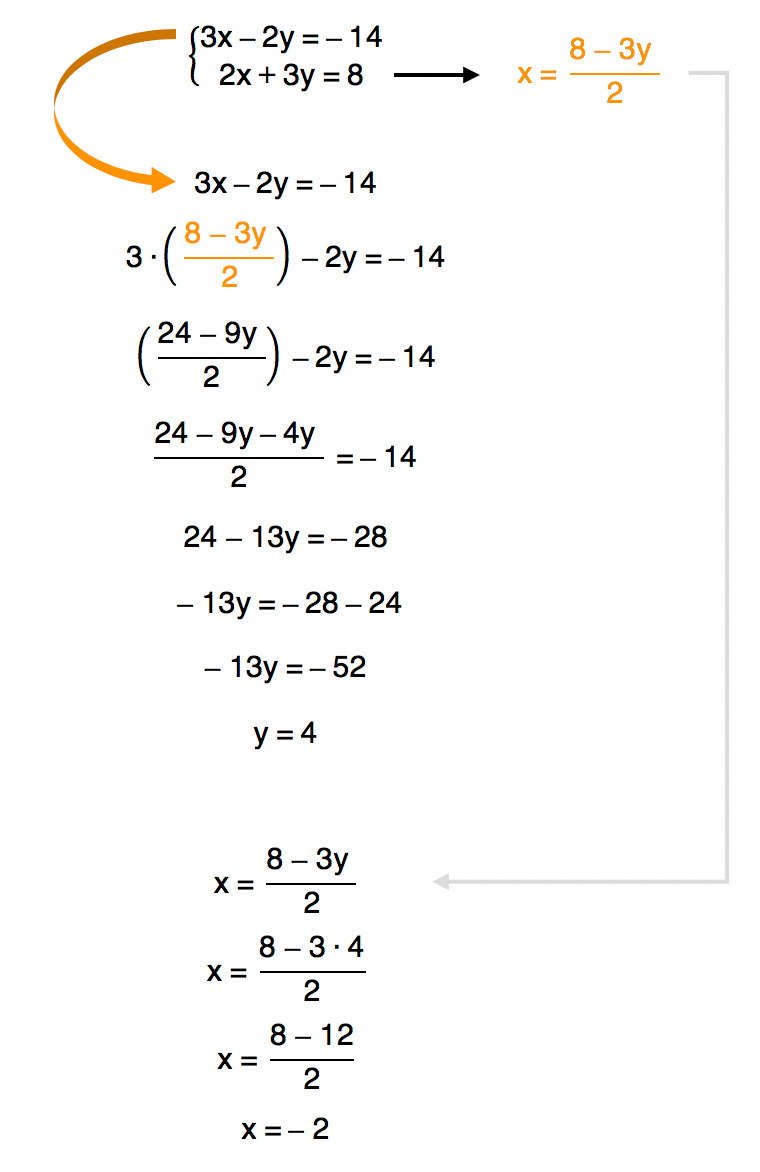
Assim, o conjunto solução do sistema Ă© dado por S = {(â 2, 4)}. Reparem, pessoal, que nesse caso nĂŁo ficou evidente nenhuma maneira mais simples de isolar a incĂłgnita x ou a incĂłgnita y no inĂcio da resolução do sistema. EntĂŁo, optou-se por seguir o caminho que vocĂȘs acabaram de conferir. Vamos analisar agora, a resolução do mesmo sistema pelo mĂ©todo da adição. Vem comigo!
Â
Método da adição
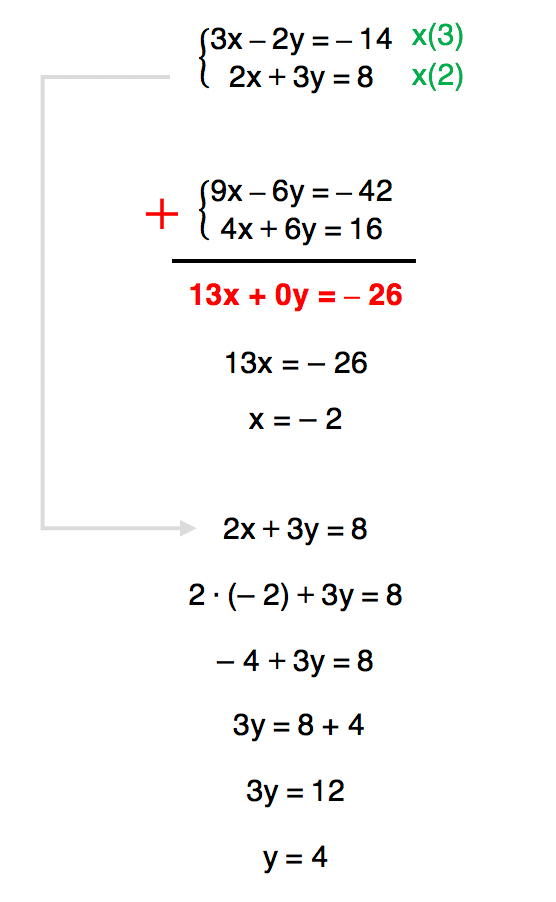
Novamente, temos como conjunto solução S = {(â 2, 4)}. Vejam que nesse caso, nenhuma das incĂłgnitas do sistema tinha coeficientes mĂșltiplos nas duas equaçÔes (3 nĂŁo Ă© mĂșltiplo de 2). Por isso, para que a soma de uma das incĂłgnitas fosse igual a zero, foi necessĂĄrio multiplicar as duas equaçÔes por fatores inteiros. VocĂȘs podem usar esse tipo de artifĂcio sempre que precisarem, pessoal!
Entendido? Apesar de parecer um pouco confuso no começo, tenho certeza de que o principal problema da resolução de sistemas de equaçÔes nĂŁo sĂŁo os mĂ©todos da adição e da substituição, mas sim, a interpretação do contexto das questĂ”es. Por isso, no vĂdeo abaixo, preparei para vocĂȘs alguns exercĂcios que envolvem os sistemas de equaçÔes em meio a contextos que exigem interpretação. Tenho certeza que essas resoluçÔes terĂŁo muito a contribuir para o aprendizado de vocĂȘs, entĂŁo, nĂŁo deixem de assistir o vĂdeo!
Gostou desse conteĂșdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemĂĄtica e ciĂȘncias da natureza? EntĂŁo conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abraço a todos, pessoal! Vejo vocĂȘs no prĂłximo post!
