EQUAÇÕES MODULARES – PARTE 1

Olá pessoal! Como vão?

As equações modulares, são todas as equações em que a incógnita aparece dentro de módulos. Isso pode parecer assustador, principalmente porque existem diversos tipos de equações modulares, mas saibam que não há motivo para se preocupar: se vocês conhecerem a definição e as propriedades do módulo, e também souberem resolver equações do primeiro e do segundo grau direitinho, então as equações modulares não serão, nem de longe, um problema lá nas provas de matemática dos vestibulares!

E falando em vestibulares, vocês sabiam que na plataforma do Professor Ferretto tem aulas de aprofundamento sobre geometria de posição e o estudo das cônicas? Sim, o curso possui aulas sobre toda a matemática do ensino médio 100% online, gravadas para que vocês possam assistir quando e onde quiserem, e também aulas ao vivo exclusivas para os assinantes. Além disso, a plataforma conta com exercícios, questões com resolução em vídeo, materiais para download, plano de estudo personalizado e até monitoria para assinantes do plano diamante. Venha conhecer a plataforma do Professor Ferretto! É só acessar o site para saber tudo sobre ela!

Bom, como foi dito no início deste texto, existem diversos tipos de equações modulares. Cada uma delas possui uma certa particularidade, por exemplo, existem equações modulares que se relacionam as equações do 1º grau, enquanto outras tem relação exclusiva com as equações do 2º grau. Hoje, a ideia é resolvermos uma série de exemplos que envolvam apenas o primeiro grau, nos quais vocês poderão se basear para solucionar outros casos parecidos. 

Então, sem mais delongas, vamos começar! Aí vem o primeiro exemplo…

1. | x – 3 | = 5

Vejam, a incógnita x está dentro de um módulo, portanto não há como negar que essa equação é modular. Agora, como é possível resolvê-la? Utilizando uma das propriedades do módulo, é claro!

Pessoal, o módulo de qualquer número real, seja ele positivo ou negativo, sempre resultará em um valor positivo! Por isso, o módulo de um certo número x, e do valor oposto a ele, – x, será exatamente igual ao próprio x. Para ficar mais claro, deem uma olhada no exemplo numérico abaixo:

Se módulo de x é igual a um certo valor numérico, que no caso do exemplo é 4, então tanto faz se x assumir o valor 4, ou o valor oposto a ele, que é – 4.  Tanto módulo de 4, quanto módulo de –4 são iguais a 4. Esse quadro é extremamente importante pessoal, porque nós utilizaremos essa mesma ideia para resolver todas as equações modulares desse texto.

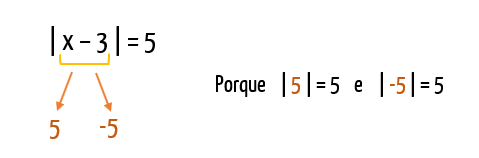
Nossa primeira equação afirma que o módulo da expressão x – 3 deve ser igual a 5. Então tanto faz se a expressão x – 3 resultar em 5 ou em –5, porque tanto módulo de 5, quanto módulo de –5 são iguais a 5! Bem louco, não é mesmo?  Assim, para encontrar a solução da equação, é preciso determinar para qual valor de x a expressão x – 3 é igual a 5, e para qual valor de x a expressão é igual a –5. É aí que entra a relação com as equações do 1º grau:

As resoluções acima, nos mostram que x pode valer 8 ou então – 2, e dessa forma a equação será verdadeira. Mas será que é verdadeira mesmo? Não custa nada verificarmos se isso está certo, substituindo a incógnita x da equação por 8 e por – 2.

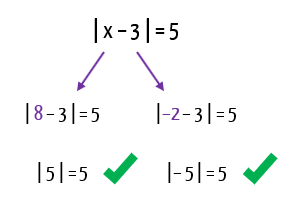
Viram como deu certo? Agora sim, podemos determinar com toda a certeza, o conjunto solução da equação:

S = {– 2, 8}

2. | 2x + 1 | = – 4

E aí, o que acharam dessa nova equação? Novamente temos a incógnita x dentro de um módulo, o que nos permite concluir que se trata de uma equação modular. Desta forma, poderíamos seguir a resolução normalmente, como no caso anterior, não fosse um pequeno, mas precioso detalhe, que não podemos deixar passar!

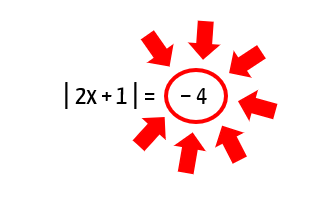
Pessoal, o módulo de qualquer número real jamais resultará em um número negativo! Isso significa que não existe nenhum valor numérico que possa substituir o lugar de x na expressão 2x + 1, e fazer com que ela resulte em um valor negativo! Quando não existem valores de x que satisfaçam uma equação, o seu conjunto solução costuma ser dado pelo conjunto vazio.

S = {   } = ∅

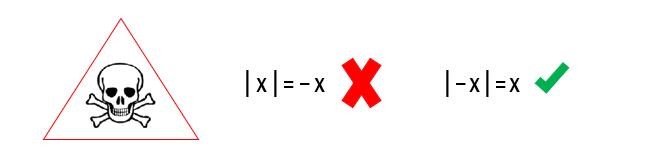
Entenderam o alerta que aparece na imagem acima? É importante lembrar sempre que não há problema algum em obtermos o módulo de um número negativo! O que não pode acontecer é que o resultado do módulo de um determinado número seja negativo. E aí vai a famosa frase mais uma vez: o módulo de qualquer número real, seja ele positivo ou negativo, sempre resultará em um valor positivo!

Beleza? Então vamos ao próximo exemplo.

3.

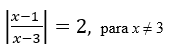
Bom, parece que nesse caso também temos uma equação modular, afinal, a incógnita x está dentro do módulo. Outro detalhe interessante, é que ao contrário do exemplo anterior esse módulo está sendo igualado a um número positivo, portanto, é provável que existam valores de x que satisfaçam essa equação. Mas aí restaria a pergunta: por que x deve ser diferente de 3?

Essa equação possui uma restrição porque é formada por uma fração, e o denominador de qualquer fração jamais pode ser zero. Mas se 3 assumisse o lugar de x, teríamos um denominador de valor zero. Por isso, seja qual for a solução encontrada, ela deve ser diferente de 3!

Tendo isso em vista, podemos perceber que o módulo da expressão que é formada pela fração deve resultar em 2. Isso significa que essa fração pode ser igual a 2 ou igual a – 2, afinal tanto módulo 2, quanto módulo de – 2 são iguais a 2, não é mesmo?

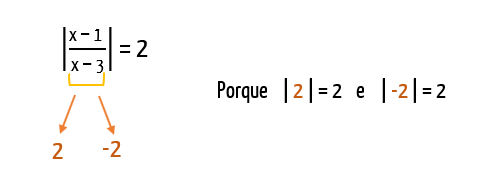
Portanto:

S = {7/3, 5}

4. | 2x – 7 | = | x + 4 |

Parece que nesse caso, não há dúvidas de que se trata de uma equação modular, afinal, temos a presença do módulo em ambos os lados da igualdade! Quando isso acontece, é necessário utilizar a seguinte propriedade:

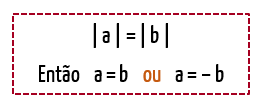
Se o módulo de a é igual ao módulo de b, então a pode ser igual a b, ou igual ao valor oposto de b, que é – b. Como no caso do exemplo, a expressão que assume o lugar de a é 2x – 7, e a expressão que assume o lugar de b é x + 4, então podemos dizer que 2x – 7 pode ser igual a x + 4, ou igual ao valor oposto de x + 4, que é –x – 4.

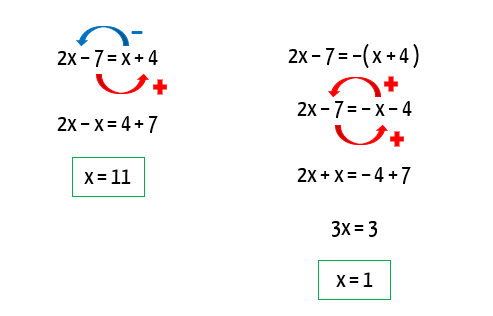
Tudo entendido? Para que uma equação como essa seja resolvida com sucesso, é importante ter em mente que obter o valor oposto de uma expressão, significa multiplicá-la inteiramente por – 1. Por isso, o oposto de x + 4 , é –x – 4, e ambos os sinais foram alterados. Assim, é possível dizer que o conjunto solução da equação é:

S = {1, 11}

E agora, vamos ao último exemplo! Mais um detalhe extremamente interessante será apresentado na sequência.

5. | x + 1 | = 2x – 6

Que estranho! A incógnita x está dentro e fora do módulo. Pois é, mas mesmo assim podem ter certeza que se trata de uma equação modular. Em casos como esse, em que existe uma expressão algébrica do lado direito da igualdade, antes de fazer qualquer análise em relação ao módulo, é necessário garantir que a mesma não resulte em um valor negativo, afinal, o módulo de qualquer número real sempre resultará em um valor positivo!

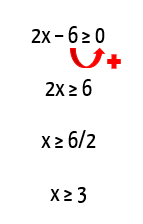
Agora, sabemos que seja qual for o conjunto solução desta equação, ele deve ser formado apenas por valores que sejam maiores ou iguais a 3, e pronto! Desta forma podemos prosseguir a análise, considerando que a expressão x + 1, que está dentro do módulo, pode ser igual a expressão 2x – 6, ou igual ao valor oposto de 2x – 6, que é –2x + 6, exatamente da mesma maneira que no exemplo anterior.

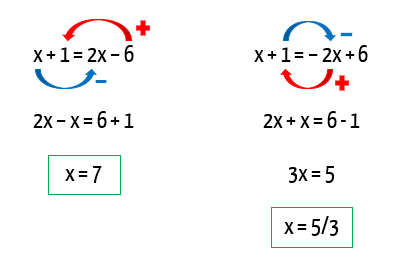
Obtidas as possíveis soluções, lá vai a pergunta: ambas são maiores ou iguais a 3? Pois é, 7 é maior que 3, mas 5/3 equivale a dízima periódica 1,66666…, que não é maior que 3. Assim, nesse caso, o conjunto solução da equação será o seguinte conjunto unitário:

S = {7}

Entendido, pessoal? É muito importante termos ciência das restrições que podem surgir nas resoluções das equações modulares. Elas podem impedir que certos valores façam parte da solução dessas equações, como acabou de acontecer. Por isso, não custa nada substituir os valores de x encontrados na equação como um todo, para garantir que a solução esteja correta, como foi feito no nosso primeiro exemplo! E já que o texto está terminando, sugiro que vocês façam isso para os demais exemplos, afim de comprovarem que ficou tudo bem claro. Como sempre, lembrem que assistir o vídeo que está em anexo também só tem a contribuir ainda mais para o conhecimento de vocês!

Até o próximo texto, pessoal! Tenham sempre bons estudos!