FUNÇÃO PAR E FUNÇÃO ÍMPAR

Olá pessoal, tudo bem com vocês?

Quando estudamos a semelhança nas representações gráficas das funções matemáticas, passamos a compreender a paridade destas funções, ou seja, quando elas podem ser classificadas como função par e como função ímpar. É claro que isso não acontece em todas as funções, mas se alguma questão de matemática lhes descrever uma função como sendo par, ou ímpar, vocês precisam saber o que isso significa, afinal, todo e qualquer acerto em uma prova de vestibular é muito bem-vindo, não é mesmo?

E por falar em vestibular, vocês sabiam que na plataforma do Professor Ferretto tem aulas de aprofundamento que abordam a matemática dos concursos de alto nível? É isso mesmo, lá vocês aprendem desde a matemática mais simples, até a mais complexa, e garantem a melhor preparação para as provas do ENEM e dos vestibulares mais tradicionais do país! Tudo isso através de videoaulas didáticas, resoluções de exercícios com foco na interpretação das questões, simulados semanais e muito mais! Acessem o site e confiram todos os benefícios do curso!

Curiosos para saber quando uma função é par ou ímpar? Então se preparem, porque a partir de hoje vocês vão ficar de olho nas semelhanças que as funções tem. Mas aí vai um aviso importante: não se preocupem caso vocês não conheçam as funções que serão apresentadas. Procurem entender o que as torna pares ou ímpares, e pronto!

 

1. FUNÇÃO PAR

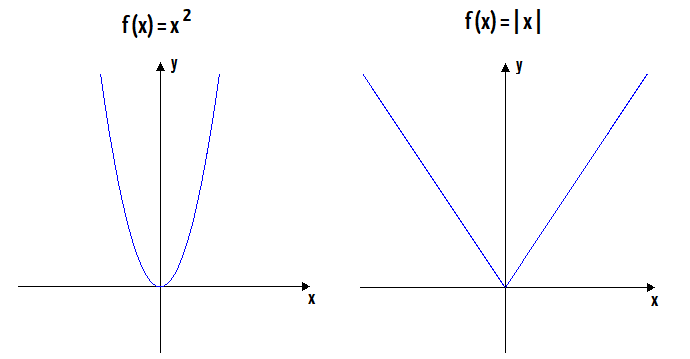
Observando cada um dos gráficos das funções acima, vocês conseguiram identificar alguma semelhança evidente? Não? Então eu vou dar uma dica: imagine agora, que você está posicionado exatamente sobre o eixo y, ou eixo das ordenadas do plano cartesiano, olhando em direção ao sentido positivo do eixo x. O que você estaria enxergando com relação ao gráfico da função?

Neste momento, suponha que você ainda está posicionado sobre o eixo y, mas agora olhando para o outro lado, na direção negativa do eixo x. O que você observa agora, em relação ao gráfico da função, não é exatamente a mesma coisa que você via quando olhava para o outro lado?  

Pois bem, essas suposições nos permitem descobrir a característica gráfica de uma função par:

Uma função f é par, quando o seu gráfico é simétrico em relação ao eixo y.

Quando uma função é par, a sua forma gráfica tem o eixo y como eixo de simetria. É como se esse eixo fosse um espelho, de maneira que o gráfico que está localizado a direita dele, é o mesmo gráfico que está localizado a sua esquerda, o mesmo! Agora, prestem atenção em alguns pontos específicos de cada uma das funções exemplo. Eles vão nos ajudar a entender a característica algébrica da função par.

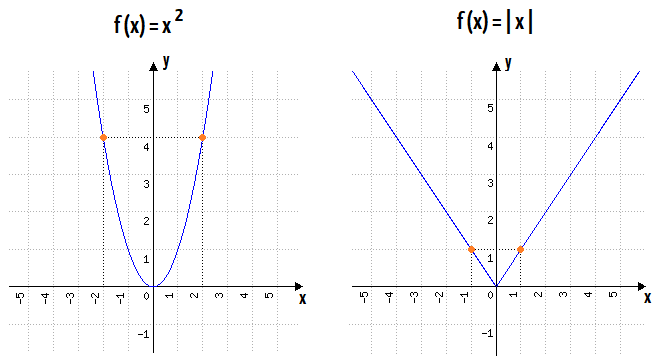
Para quem não está familiarizado com as funções acima, f(x) = x² é uma função quadrática, enquanto que a função f(x) = | x |, é conhecida como função modular. No gráfico da função quadrática, vemos que dois pontos específicos foram ressaltados, (2, 4) e (–2, 4). Reparem então, que os valores da coordenada x desses dois pontos, são simétricos ou opostos, isto é, são valores de mesmo módulo, porém de sinais contrários. Mas o que chama mais atenção é que o valor da coordenada y é exatamente igual nos dois pontos. Isso significa que ao substituir o valor de x nas funções pares, por valores simétricos ou opostos, obtém-se o mesmo valor respectivo em y. Em outras palavras, dois valores simétricos ou opostos do domínio de uma função par, possuem exatamente a mesma imagem!

E não é que isso acontece na função modular também? Claro né, ela é uma função par! Vejam que nos dois pontos que foram ressaltados, a imagem, ou o valor da coordenada y é o mesmo, 1, enquanto os seus respectivos valores de x, ou do domínio da função, são valores simétricos ou opostos, –1 e 1. Isso irá acontecer para todo e qualquer valor de x e seu simétrico, sem exceção, como mostra a tabela abaixo:

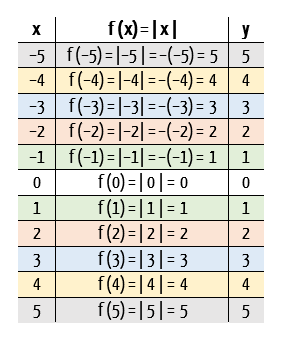
Assim, como foi dito anteriormente, essa análise nos permite compreender a característica algébrica da função par:

Uma função f é par, se f(x) = f(–x).

Então pessoal, a condição f(x) = f(–x) caracteriza uma função par. Por isso, quando for preciso averiguar se uma função é par através do método algébrico, basta substituir x por –x, e verificar se o resultado é igual ao da função f(x) inicial. Olhem só:

f(x) = x²

f(–x) = (–x)² = x²

Quando um valor negativo é elevado a um expoente par, o resultado certamente é positivo. Por isso f(–x), nesse caso, também resultou em x², que é o valor da própria f(x) inicial. Então, f(x) = f(–x), e a condição para que a função seja par foi satisfeita!

Quanto a função modular f(x) = | x |, é fato que existe até uma propriedade que diz que para todo x ∈ ℝ, | x | = | –x |. Por isso, é possível dizer sim que f(x) = f(–x), e fica comprovado algebricamente que essa função é mesmo par!

f(x) = | x | = x

f(–x) =  | –x | = –(–x) = x

Pessoal, não se preocupem tanto com os termos algébricos. Também é possível fazer esse teste com valores numéricos, e posso jurar pra vocês que nós já fizemos isso nas tabelas acima. Se vocês substituírem x em uma função, por dois quaisquer valores numéricos simétricos ou opostos, e o resultado for o mesmo, não haverá como negar que tal função é par!

 

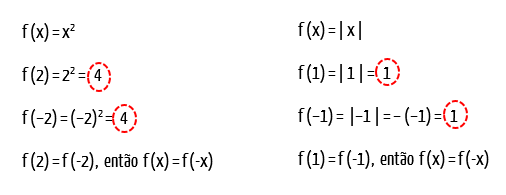
2. FUNÇÃO ÍMPAR

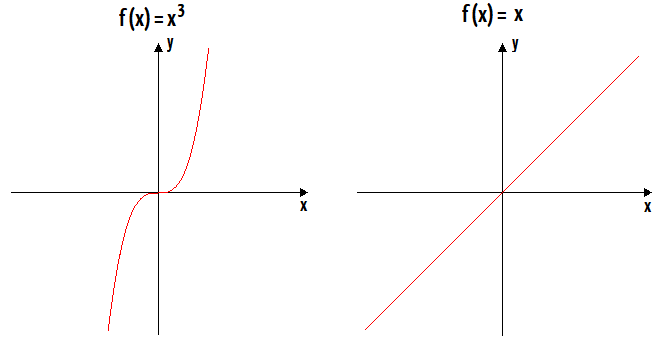
Se vocês captaram a ideia anterior, para encontrar a semelhança dos gráficos acima, provavelmente chegaram bem perto do que caracteriza graficamente uma função ímpar. Mas já aviso, de antemão, que não vai adiantar nada se posicionar no eixo y para visualizar esses gráficos. Olhem só o que vocês precisarão fazer para encontrar a simetria nesse caso:

Exatamente! Agora quem se torna um espelho para os gráficos é a origem do plano cartesiano. Isso nos permite concluir que:

 Uma função f é ímpar, quando o seu gráfico é simétrico em relação à origem.

 

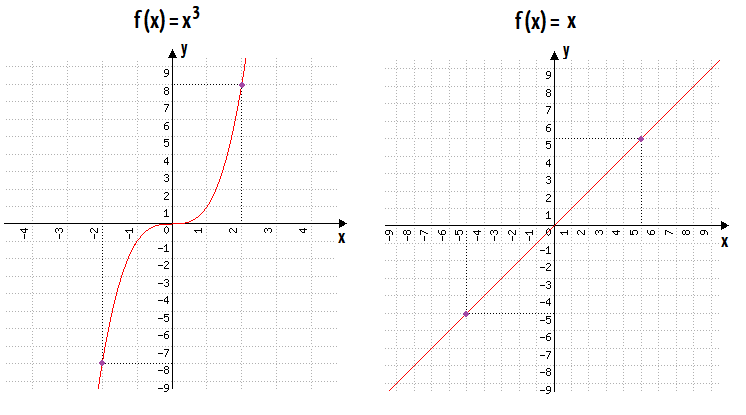
Para quem não nunca viu as funções acima, f(x) = x é uma função do 1º grau, muito conhecida também como função identidade. Já função f(x) = x³, pode ser dita como uma função cúbica. No gráfico da função identidade, nós vemos que os dois pontos ressaltados foram (5, 5) e (–5, –5). Reparem então, que os valores da coordenada x desses dois pontos também são simétricos ou opostos, isto é, são valores de mesmo módulo, porém de sinais contrários. Mas o que nos surpreende aqui, é que os valores da coordenada y de cada ponto também são simétricos ou opostos. Isso significa que ao substituir o valor de x nas funções ímpares, por valores simétricos ou opostos, obtém-se valores respectivos em y também simétricos. Em outras palavras, dois valores simétricos ou opostos do domínio de uma função ímpar, possuem imagens também simétricas ou opostas!

Bom, na função cúbica não poderia ser diferente. Vejam que nos dois pontos que foram ressaltados, tanto os valores do domínio da função, –2 e 2, quanto os respectivos valores da imagem de f(x) = x³, ou seja, –8 e 8, são opostos ou simétricos. Isso irá acontecer para todo e qualquer valor de x e seu simétrico, sem exceção, como mostra a tabela abaixo:

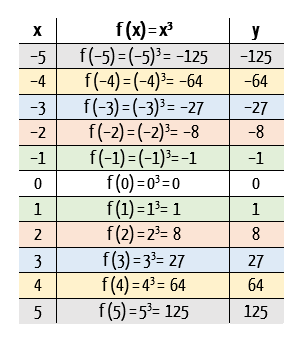
Então, presumo que vocês imaginem qual será a característica algébrica da função ímpar:

Uma função f é ímpar, se f(x) = –f(–x).

Parece que agora ficou complicado comprovar algebricamente que uma função é ímpar, não é mesmo? Pessoal, não muda quase nada, acreditem! Vocês vão continuar substituindo x por –x, só que agora, o resultado deve ser o mesmo em módulo, mas de sinal contrário ao da função f(x) inicial. Olhem só como fica a situação das funções do nosso exemplo:

f(x) = x

f(–x) = –x

 

f(x) = x³

f(–x) = (– x)³ = – x³

Quando um valor negativo é elevado a um expoente ímpar, o resultado permanece negativo. E felizmente para nós, nos dois casos o valor de f(–x) foi exatamente igual ao de f(x), só que com o sinal contrário. Portanto f(x) = –f(–x), e a condição para que a função seja ímpar foi satisfeita!

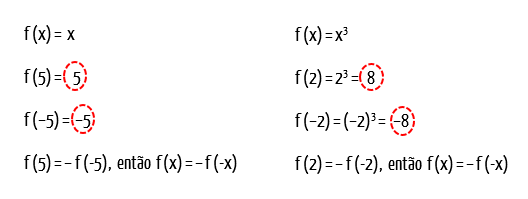
E para provar que eu não menti lá no início do texto, olhem só essa observação aqui:

Um exemplo de função que não é ímpar e nem par, é esta aqui:

f(x) = 2x –1

Para comprovar algebricamente que f(x) = 2x –1 não é par e nem ímpar, basta substituir x por –x. A função gerada não poderá ser igual a função f(x) inicial, o que caracterizaria uma função par, e nem mesmo ser igual em módulo mas de sinal contrário a f(x) inicial, porque isso caracterizaria uma função ímpar. Então vamos ver logo o que acontece com essa função:

f(x) = 2x –1

f(–x) = 2∙(–x) –1 = –2x –1

Bom, é fato que –2x –1 ≠ 2x –1, então sem chance dessa função ser par. Da mesma forma que não podemos negar que –(–2x –1) ≠ 2x –1, e aí a condição para que a função seja ímpar também não é satisfeita. Querem mais uma prova? Então deem uma olhada no gráfico da função f(x) = 2x –1:

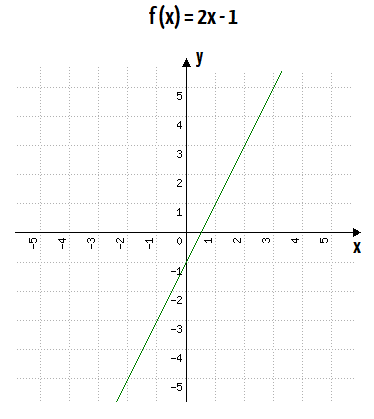
E aí, tem simetria em relação ao eixo y? E em relação à origem do plano cartesiano, tem? Não tem simetria coisa nenhuma! Desta forma, f(x) = 2x –1 não é, comprovadamente, nem uma função par, e nem uma função ímpar.

Pessoal, no vídeo que deixo em anexo, tem mais um monte de funções para vocês comprovarem, junto comigo, se são pares, ímpares, ou nenhuma das duas coisas. Portanto, não dá para deixar de ver! E infelizmente por hoje é só, vamos ter que encerrar o texto por aqui. Mas espero que vocês tenham gostado do assunto, e que a partir de hoje, consigam identificar funções pares e ímpares com mais facilidade!

Um abração e tenham sempre ótimos estudos!