APLICANDO A LOGARITMAÇÃO

Olá pessoal! Como vão?

Hoje vamos aprender a aplicar uma operação muito importante para a matemática, que chamamos de logaritmação. Isso significa, já que o termo é um pouco confuso, que nós vamos resolver logaritmos, inúmeros deles! É muito importante que vocês se familiarizem com a operação dos logaritmos, pois ela costuma ser cobrada nas provas dos vestibulares e do ENEM.

Se vocês quiserem ter acesso a um material completo sobre logaritmos, com exercícios resolvidos e muitos exercícios de vestibulares e do ENEM disponíveis, assinem a plataforma do Professor Ferretto! É uma plataforma completa, com todo o conteúdo de matemática do ensino médio, videoaulas, plano de estudos e muito mais! Acessem o site para conferir todos os serviços oferecidos!

Vamos começar revisando como podemos resolver os logaritmos. Vem comigo aqui!

 

1. LOGARITMAÇÃO

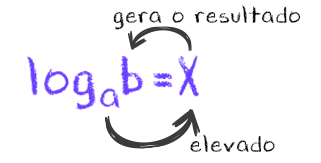
Vocês já viram algo semelhante a figura acima? Pois é, no texto Introdução aos Logaritmos, nós vimos que essa é a maneira de resolver um logaritmo, ou seja, de aplicar a logaritmação, que é apresentada abaixo:

Aplicando essas setinhas no nosso logaritmo, nós podemos lembrar facilmente que a base a, deve ser elevada ao logaritmo x, ou seja, deve ter como expoente o x, e o resultado disso é o logaritmando b. Assim é possível transformar a expressão log_a b = x na expressão a ^x = b, e vice-versa.

É importante lembrar também que a base a e o logaritmando b possuem algumas restrições quanto aos valores que podem assumir. Tanto a como b, devem ser valores positivos ou maiores do que zero, e ainda, a deve ser diferente de um. Portanto 0 < a ≠ 1 e b > 0. Para ver tudo isso de forma detalhada, e para revisar o conceito dos termos base, logaritmando e logaritmo, eu aconselho vocês a darem uma olhadinha no texto Introdução aos Logaritmos. Assim vocês ficarão ainda mais seguros para resolver qualquer questão como essas que faremos agora.

     1. Determine os seguintes logaritmos:

      

O primeiro passo aqui é igualarmos esse logaritmo a incógnita que desejarmos, pois ela será o nosso resultado. Aqui nós vamos utilizar a incógnita x, olhem só:

O segundo passo é observamos se os valores da base e do logaritmando estão de acordo com as restrições impostas sobre eles. Vejam que a nossa base aqui é o número 2, um valor positivo e diferente de 1. Da mesma forma, o valor do nosso logaritmando, 128, também é positivo, ou seja, nesse caso, não há impedimento algum para que possamos efetuar nosso cálculo.

Aí vocês poderiam questionar, mas e o valor de x, do logaritmo, não tem restrição alguma? A resposta é que não tem mesmo! O x pode ser zero, pode ser um valor negativo, pode ser um valor positivo, enfim pode ser qualquer número real.

Chegou a hora em que aplicamos as setinhas ao logaritmo, e aí obtemos a seguinte expressão:

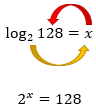
Agora, a ideia é obtermos uma igualdade de potências de mesma base, como já aprendemos lá nas Equações Exponenciais. Para isso, vamos fatorar o termo 128, e reduzi-lo a uma potência de base 2, vejam só:

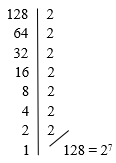
Descobrimos que 128 = 2⁷. Então, só resta-nos voltar a expressão anterior, e como vamos ter potências de mesma base, poderemos trabalhar apenas com os expoentes:

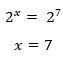
Tranquilo né pessoal? Vamos seguir com nossos exercícios, mas antes gostaria de reforçar mais uma ideia. Como estamos transformando nossos logaritmos em expressões exponenciais, novamente vamos utilizar muito as propriedades da potenciação. Por isso trago abaixo uma tabelinha para que vocês revisem todas elas!

      

Lembram de todos os passos que utilizamos para resolver a questão anterior? Vamos utilizá-los novamente. Vejam que tanto a base, como o logaritmando desse logaritmo estão de acordo com as restrições. Podemos então igualar a expressão a incógnita x, e em seguida aplicar as setinhas:

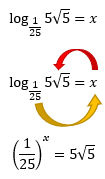
Chegamos a nossa expressão exponencial, e a ideia agora é buscar o auxílio das propriedades da potenciação que vimos na tabela, para que possamos chegar a uma igualdade de potências de mesma base. Reparem que no lado esquerdo da igualdade temos uma fração, onde o denominador é 25. 25 é uma potência de 5, porque 5² = 25, então podemos substituir esse termo na equação. Do outro lado, temos uma raiz quadrada de 5. Isso parece um problema não é? Mas se vocês repararem na nossa tabela, temos uma propriedade que nos permite transformar um radical em uma potência com expoente fracionário, a propriedade 8. Vamos aplica-la ao lado direito da equação:

Agora, sem problema algum, nós podemos utilizar no lado esquerdo da equação, a propriedade 6, que nos permitirá eliminar aquela fração. Já no lado direito, vejam que temos uma multiplicação de potências de mesma base. Isso nos remete a propriedade número 1, lembrando claro que quando um expoente não aparece, significa que ele vale 1, vejam só:

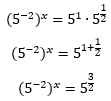
O último passo para obtermos uma igualdade de potências de mesma base, e assim, podermos igualar os expoentes, é aplicar a propriedade 3 ao lado esquerdo da equação, naquela potência de potência:

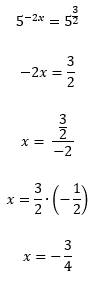
Certo pessoal? Vamos agora ao nosso exercício 2, onde precisaremos resolver mais de um logaritmo em uma mesma equação.

     2.Calcule o valor de A:

     

Em casos como esse, é necessário que façamos a resolução de cada logaritmo separadamente, para depois voltarmos a expressão original. Assim, nós chamaremos de x o resultado do primeiro logaritmo, enquanto que o do segundo nós chamaremos de y. Mas vocês repararam que há algo diferente nesses logaritmos? Qual é valor de suas bases?

No texto Introdução aos Logaritmos, nós também estudamos que quando a base de um logaritmo não aparece, significa que ele é um logaritmo decimal, ou seja, sua base vale 10. Dessa forma podemos dizer que:

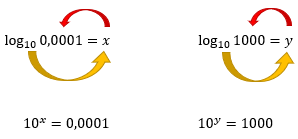
Se observarmos agora, no lado direito de ambas as equações, nós temos potências de base 10. Andando 4 casas para a direita, no primeiro caso, sabemos que 0,0001 = 10^-4, ao mesmo tempo que, se andarmos 3 casas para a esquerda, no segundo caso, podemos dizer que 1000 = 10³, e assim, temos:

Voltando a nossa expressão inicial:

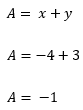
Gostaram desse exemplo? Vamos a mais um caso semelhante!

     

E agora, como resolver uma situação como essa? Vamos usar a mesma ideia do exemplo anterior, resolvendo cada caso separadamente. Iniciaremos sempre pelo logaritmo que está dentro do parênteses, olhem só:

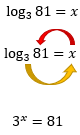
Fatorando o número 81, nós descobrimos que 81 = 3⁴. Então:

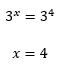
Já temos o valor de x, então podemos voltar a nossa expressão inicial:

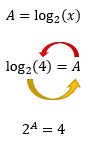
Como sabemos que 4 = 2²:

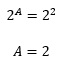
Estamos quase no fim do nosso texto! Mas antes, gostaria de mostrar para vocês dois exemplos um pouquinho diferentes daqueles que já fizemos, onde as restrições impostas a base e ao logaritmando serão ainda mais importantes. Vamos lá!

     3. Determine o valor de x:

     

Que coisa mais interessante, vocês observaram que dessa vez a nossa incógnita está na base? Não se assustem, a resolução é igualzinha à anterior. A única diferença é que depois de obtermos o resultado, teremos que avaliar se ele está de acordo com as restrições ou não. Querem ver como fica?

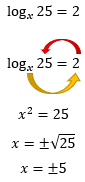
Temos dois resultados possíveis, x₁ = +5 e x₂ = -5. Contudo, a base x, deve ser um valor maior que zero e diferente de um (0 < x ≠ 1). Isso significa que devemos descartar o resultado x₂, porque ele é um valor negativo, e assim nossa resposta é unicamente:

Entendido? Vamos ao nosso último caso:

     

Novamente, a ideia é resolver a questão normalmente e depois avaliar se a solução encontrada é possível ou não. Vamos lá:

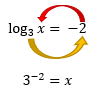
Aplicando a propriedade da potenciação número 6, nós temos que:

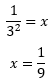
A incógnita x, nesse caso, estava localizada no logaritmando, certo? Nós sabemos que o logaritmando deve ser sempre positivo, ou maior que zero (x > 0). Aí fica a pergunta: 1/9 é maior que zero? É! Então nossa resposta é mesmo:

Chegamos ao final de mais um texto, e eu espero que todos os exemplos mostrados aqui tenham sido muito proveitosos, para que vocês apliquem tudo o que aprenderam nas provas que irão fazer! Deixo em anexo, um vídeo contendo mais alguns exercícios resolvidos para vocês revisarem bem o conteúdo.

Abração! Sucesso na caminhada e até mais!